题目内容
(2012•新疆)为了解“阳光体育”活动情况,我市教育部门在市三中2000名学生中,随机抽取了若干学生进行问卷调查(要求每位学生只能填写一种自己喜欢的活动),并将调查的结果绘制成如图的两幅不完整的统计图:
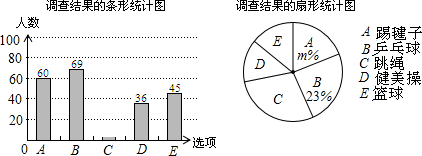
根据以上信息解答下列问题:
(1)参加调查的人数共有
(2)补全条形统计图,并计算扇形统计图中的m;
(3)若要从该校喜欢“B”项目的学生中随机选择100名,则喜欢该项目的小华同学被选中的概率是多少?

根据以上信息解答下列问题:
(1)参加调查的人数共有
300
300
人;在扇形图中,表示“C”的扇形的圆心角为108
108
度;(2)补全条形统计图,并计算扇形统计图中的m;
(3)若要从该校喜欢“B”项目的学生中随机选择100名,则喜欢该项目的小华同学被选中的概率是多少?
分析:(1)用喜欢乒乓球的人数除以其所占的百分比即可求得调查的总人数;
(2)用喜欢C项目的人数除以总人数即可求得其百分率,从而得到m的值;
(3)求出喜欢B类项目的总人数,利用概率公式即可求得该同学被抽中的概率.
(2)用喜欢C项目的人数除以总人数即可求得其百分率,从而得到m的值;
(3)求出喜欢B类项目的总人数,利用概率公式即可求得该同学被抽中的概率.
解答:解:(1)观察统计图知喜欢乒乓球的有69人,占总人数的23%,
故调查的总人数有69÷23%=300人,
喜欢跳绳的有300-60-69-36-45=90人,
故C所表示的扇形的圆心角为
×360°=108°;
(2)m%=
×100%=20%,故m=20

(3)喜欢B项目的有2000×
=460人,
故小华被抽中的概率为
=
.
故调查的总人数有69÷23%=300人,
喜欢跳绳的有300-60-69-36-45=90人,
故C所表示的扇形的圆心角为
| 90 |
| 300 |
(2)m%=
| 60 |
| 300 |

(3)喜欢B项目的有2000×
| 69 |
| 300 |
故小华被抽中的概率为
| 100 |
| 460 |
| 5 |
| 23 |
点评:本题考查了条形统计图的知识,解题的关键是仔细的观察两种统计图,并结合两种统计图得到进一步解题的有关信息.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
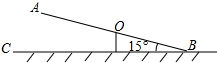 (2012•新疆)如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为15°,且OA=OB=3m.
(2012•新疆)如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为15°,且OA=OB=3m.