题目内容
(2012•新疆)库尔勒某乡A,B两村盛产香梨,A村有香梨200吨,B村有香梨300吨,现将这些香梨运到C,D两个冷藏仓库.已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C,D两处的费用分别为每吨40元和45元;从B村运往C,D两处的费用分别为每吨25元和32元.设从A村运往C仓库的香梨为x吨,A,B两村运香梨往两仓库的运输费用分别为yA元,yB元.
(1)请填写下表,并求出yA,yB与x之间的函数关系式;
(2)当x为何值时,A村的运费较少?
(3)请问怎样调运,才能使两村的运费之和最小?求出最小值.
(1)请填写下表,并求出yA,yB与x之间的函数关系式;
| C | D | 总计 | |
| A | x吨 | 200吨 | |
| B | 300吨 | ||
| 总计 | 240吨 | 260吨 | 500吨 |
(3)请问怎样调运,才能使两村的运费之和最小?求出最小值.
分析:(1)由A村共有香梨200吨,从A村运往C仓库x吨,剩下的运往D仓库,故运往D仓库为(200-x)吨,由A村已经运往C仓库x吨,C仓库可储存240吨,故B村应往C仓库运(240-x)吨,剩下的运往D仓库,剩下的为300-(240-x),化简后即可得到B村运往D仓库的吨数,填表即可,由从A村运往C,D两处的费用分别为每吨40元和45元;从B村运往C,D两处的费用分别为每吨25元和32元,由表格中的代数式,即可分别列出yA,yB与x之间的函数关系式;
(2)由第一问表示出的yA与x之间的函数关系式得到此函数为一次函数,根据x的系数为负数,得到此一次函数为减函数,且0≤x≤200,故x取最大200时,yA有最小值,即为A村的运费较少时x的值;
(3)设两村的运费之和为W,W=yA+yB,把第一问表示出的两函数解析式代入,合并后得到W为关于x的一次函数,且x的系数大于0,可得出此一次函数图象是y随x的增大而增大,可得出x=0时,W有最小值,将x=0代入W关于x的函数关系式中,即可求出W的最小值.
(2)由第一问表示出的yA与x之间的函数关系式得到此函数为一次函数,根据x的系数为负数,得到此一次函数为减函数,且0≤x≤200,故x取最大200时,yA有最小值,即为A村的运费较少时x的值;
(3)设两村的运费之和为W,W=yA+yB,把第一问表示出的两函数解析式代入,合并后得到W为关于x的一次函数,且x的系数大于0,可得出此一次函数图象是y随x的增大而增大,可得出x=0时,W有最小值,将x=0代入W关于x的函数关系式中,即可求出W的最小值.
解答:解:(1)填写如下:
由题意得:yA=40x+45(200-x)=-5x+9000;yB=25(240-x)+32(60+x)=7x+7920;
(2)∵-5x+9000<x+7920,
解得:x>180,
∴当x>180时,A村的运费较少;
(3)设两村的运费之和为W,
则W=yA+yB=-5x+9000+7x+7920=2x+16920(0≤x≤200),
∵k=2>0,
∴此一次函数为增函数,
则当x=0时,W有最小值,W最小值为16920元.
此时调运方案为:从A村运往C仓库0吨,运往D仓库为200吨,B村应往C仓库运240吨,运往D仓库60吨.
| C | D | 总计 | |
| A | x吨 | (200-x)吨 | 200吨 |
| B | (240-x)吨 | (60+x)吨 | 300吨 |
| 总计 | 240吨 | 260吨 | 500吨 |
(2)∵-5x+9000<x+7920,
解得:x>180,
∴当x>180时,A村的运费较少;
(3)设两村的运费之和为W,
则W=yA+yB=-5x+9000+7x+7920=2x+16920(0≤x≤200),
∵k=2>0,
∴此一次函数为增函数,
则当x=0时,W有最小值,W最小值为16920元.
此时调运方案为:从A村运往C仓库0吨,运往D仓库为200吨,B村应往C仓库运240吨,运往D仓库60吨.
点评:此题考查了一次函数的应用,涉及的知识有:一次函数的性质,以及函数关系式的列法,解答一次函数的应用问题中,要注意自变量的取值范围还必须使实际问题有意义.本题注意x的范围为0≤x≤200.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
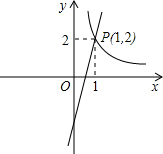 (2012•新疆)如图,一次函数y=kx-3的图象与反比例函数
(2012•新疆)如图,一次函数y=kx-3的图象与反比例函数