题目内容
(2012•新疆)如图1,在直角坐标系中,已知△AOC的两个顶点坐标分别为A(2,0),C(0,2).
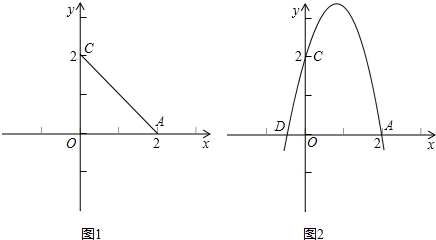
(1)请你以AC的中点为对称中心,画出△AOC的中心对称图形△ABC,此图与原图组成的四边形OABC的形状是
(2)如图2,已知D(-
,0),过A,C,D的抛物线与(1)所得的四边形OABC的边BC交于点E,求抛物线的解析式及点E的坐标;
(3)在问题(2)的图形中,一动点P由抛物线上的点A开始,沿四边形OABC的边从A-B-C向终点C运动,连接OP交AC于N,若P运动所经过的路程为x,试问:当x为何值时,△AON为等腰三角形(只写出判断的条件与对应的结果)?

(1)请你以AC的中点为对称中心,画出△AOC的中心对称图形△ABC,此图与原图组成的四边形OABC的形状是
正方形
正方形
,请说明理由;(2)如图2,已知D(-
| 1 | 2 |
(3)在问题(2)的图形中,一动点P由抛物线上的点A开始,沿四边形OABC的边从A-B-C向终点C运动,连接OP交AC于N,若P运动所经过的路程为x,试问:当x为何值时,△AON为等腰三角形(只写出判断的条件与对应的结果)?
分析:(1)按照中心对称图形的定义作图即可,易知四边形OABC为正方形;
(2)已知A、C、D三点的坐标,利用待定系数法求出抛物线的解析式;由直线BC:y=2,代入抛物线解析式解方程求得点E的坐标;
(3)在点P的运动过程中,△AON为等腰三角形的情形有三种,注意不要漏解.充分利用正方形、等腰三角形的性质,容易求得点P运动的路程x.
(2)已知A、C、D三点的坐标,利用待定系数法求出抛物线的解析式;由直线BC:y=2,代入抛物线解析式解方程求得点E的坐标;
(3)在点P的运动过程中,△AON为等腰三角形的情形有三种,注意不要漏解.充分利用正方形、等腰三角形的性质,容易求得点P运动的路程x.
解答: 解:(1)设AC的中点为E,连接OE并延长至B,使得BE=OE;连接AC,AB,则△ABC为所求作的△AOC的中心对称图形.
解:(1)设AC的中点为E,连接OE并延长至B,使得BE=OE;连接AC,AB,则△ABC为所求作的△AOC的中心对称图形.
∵A(2,0),C(0,2),∴OA=OC,
∵△ABC是△AOC的中心对称图形,∴AB=OC,BC=OA,
∴OA=AB=BC=OC,
∵∠COA=90°,
∴四边形OABC是正方形;
(2)设经过点A、C、D的抛物线解析式为y=ax2+bx+c,
∵A(2,0),C(0,2),D(-
,0),
∴
,解得a=-2,b=3,c=2,
∴抛物线的解析式为:y=-2x2+3x+2;
由(1)知,四边形OABC为正方形,∴B(2,2),
∴直线BC的解析式为y=2,
令y=-2x2+3x+2=2,解得x1=0,x2=
,
∴点E的坐标为(
,2).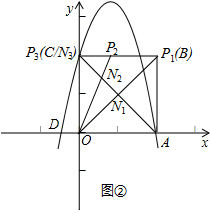
(3)在点P的运动过程中,有三种情形使得△AON为等腰三角形,
如图②所示:
①△AON1.此时点P与点B重合,点N1是正方形OABC对角线的交点,且△AON1为等腰直角三角形,
则此时点P运动路程为:x=AB=2;
②△AON2.此时点P位于B-C段上.
∵正方形OABC,OA=2,∴AC=2
,
∵AN2=OA=2,∴CN2=AC-AN2=2
-2.
∵AN2=OA,∴∠AON2=∠AN2O,
∵BC∥OA,∴∠AON2=∠CP2N2,又∠AN2O=∠CN2P2,
∴∠CN2P2=∠CP2N2,
∴CP2=CN2=2
-2.
此时点P运动的路程为:x=AB+BC-CP2=2+2-(2
-2)=6-2
;
③△AON3.此时点P到达终点C,P、C、N三点重合,△AON3为等腰直角三角形,
此时点P运动的路程为:x=AB+BC=2+2=4.
综上所述,当x=2,x=6-2
或x=4时,△AON为等腰三角形.
 解:(1)设AC的中点为E,连接OE并延长至B,使得BE=OE;连接AC,AB,则△ABC为所求作的△AOC的中心对称图形.
解:(1)设AC的中点为E,连接OE并延长至B,使得BE=OE;连接AC,AB,则△ABC为所求作的△AOC的中心对称图形.∵A(2,0),C(0,2),∴OA=OC,
∵△ABC是△AOC的中心对称图形,∴AB=OC,BC=OA,
∴OA=AB=BC=OC,
∵∠COA=90°,
∴四边形OABC是正方形;
(2)设经过点A、C、D的抛物线解析式为y=ax2+bx+c,
∵A(2,0),C(0,2),D(-
| 1 |
| 2 |
∴
|
∴抛物线的解析式为:y=-2x2+3x+2;
由(1)知,四边形OABC为正方形,∴B(2,2),
∴直线BC的解析式为y=2,
令y=-2x2+3x+2=2,解得x1=0,x2=
| 3 |
| 2 |
∴点E的坐标为(
| 3 |
| 2 |

(3)在点P的运动过程中,有三种情形使得△AON为等腰三角形,
如图②所示:
①△AON1.此时点P与点B重合,点N1是正方形OABC对角线的交点,且△AON1为等腰直角三角形,
则此时点P运动路程为:x=AB=2;
②△AON2.此时点P位于B-C段上.
∵正方形OABC,OA=2,∴AC=2
| 2 |
∵AN2=OA=2,∴CN2=AC-AN2=2
| 2 |
∵AN2=OA,∴∠AON2=∠AN2O,
∵BC∥OA,∴∠AON2=∠CP2N2,又∠AN2O=∠CN2P2,
∴∠CN2P2=∠CP2N2,
∴CP2=CN2=2
| 2 |
此时点P运动的路程为:x=AB+BC-CP2=2+2-(2
| 2 |
| 2 |
③△AON3.此时点P到达终点C,P、C、N三点重合,△AON3为等腰直角三角形,
此时点P运动的路程为:x=AB+BC=2+2=4.
综上所述,当x=2,x=6-2
| 2 |
点评:本题综合考查了待定系数法求二次函数解析式、旋转变换作图、正方形、等腰三角形、解一元二次方程等重要知识点.第(3)问是动点型问题,△AON为等腰三角形的情形有三种,注意不要漏解.作为中考压轴题,本题难度不大,有利于基础扎实的考生获得好成绩.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 (2012•新疆)如图所示,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积
(2012•新疆)如图所示,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积 (2012•新疆)如图,一次函数y=kx-3的图象与反比例函数
(2012•新疆)如图,一次函数y=kx-3的图象与反比例函数 (2012•新疆)如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为15°,且OA=OB=3m.
(2012•新疆)如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为15°,且OA=OB=3m. (2012•新疆)如图,圆内接四边形ABDC,AB是⊙O的直径,OD⊥BC于E.
(2012•新疆)如图,圆内接四边形ABDC,AB是⊙O的直径,OD⊥BC于E.