题目内容
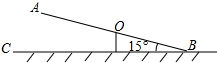 (2012•新疆)如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为15°,且OA=OB=3m.
(2012•新疆)如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为15°,且OA=OB=3m.(1)求此时另一端A离地面的距离(精确到0.1m);
(2)若跷动AB,使端点A碰到地面,请画出点A运动的路线(不写画法,保留画图痕迹),并求出点A运动路线的长.
(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)
分析:(1)过A作AD⊥BC于点D,根据比例关系及三角函数值可得出AD的值.
(2)根据出OA的长,求出∠AOD的度数,然后利用弧长的计算公式即可得出答案.
(2)根据出OA的长,求出∠AOD的度数,然后利用弧长的计算公式即可得出答案.
解答: 解:(1)过A作AD⊥BC于点D,
解:(1)过A作AD⊥BC于点D,
∵OA=OB=3m,
∴AB=3+3=6m,
∴AD=AB•sin15°≈6×0.26≈1.6;
(2)如图所示,A点的运动路线是以点O为圆心,以OA的长为半径的
的长.
连接OD,
∵O是AB的中点,
∴OD=OA=OB,
∴∠AOD=2∠B=30°,
∴A运动路线长=
=
.
 解:(1)过A作AD⊥BC于点D,
解:(1)过A作AD⊥BC于点D,∵OA=OB=3m,
∴AB=3+3=6m,
∴AD=AB•sin15°≈6×0.26≈1.6;
(2)如图所示,A点的运动路线是以点O为圆心,以OA的长为半径的
 |
| AD |
连接OD,
∵O是AB的中点,
∴OD=OA=OB,
∴∠AOD=2∠B=30°,
∴A运动路线长=
| 30×π×3 |
| 180 |
| π |
| 2 |
点评:本题考查的是解直角三角形的应用及弧长公式,根据题意作出辅助线,利用锐角三角函数的定义求解是解答此题的关键.

练习册系列答案
相关题目
 (2012•新疆)如图所示,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积
(2012•新疆)如图所示,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积 (2012•新疆)如图,一次函数y=kx-3的图象与反比例函数
(2012•新疆)如图,一次函数y=kx-3的图象与反比例函数 (2012•新疆)如图,圆内接四边形ABDC,AB是⊙O的直径,OD⊥BC于E.
(2012•新疆)如图,圆内接四边形ABDC,AB是⊙O的直径,OD⊥BC于E.