题目内容
【题目】如图,在ABCD中,点E是DC的中点,连接AE,并延长交BC的延长线于点F.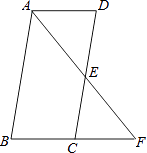
(1)求证:△ADE和△CEF的面积相等;
(2)若AB=2AD,试说明AF恰好是∠BAD的平分线.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠F,
∵点E是DC的中点,
∴CE=DE,
在△AED和△FEC中 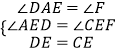 ,
,
∴△AED≌△FEC(AAS),
∴△ADE和△CEF的面积相等
(2)解:∵四边形ABCD是平行四边形,
∴AD=BC,
∵△AED≌△FEC,
∴AD=CF,
∴AD=BC=CF,
∵AB=2AD,
∴AB=2BC=BF,
∴∠BAF=∠F,
又∵∠DAE=∠F,
∴∠BAF=∠DAE,
即AF是∠BAD的平分线.
【解析】(1)根据平行四边形的性质得出AD∥BC,由平行证得角相等,然后再证明△AED≌△FEC,即可得出结论。
(2)根据平行四边形和全等三角形的性质得出AD=BC=CF,根据已知易证得AB=BF,根据等边对等角及∠DAE=∠F,从而可得到AF是∠BAD的平分线。
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线,以及对平行四边形的性质的理解,了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目





