��Ŀ����
����Ŀ�����κ���![]() ��ͼ��y����C������
��ͼ��y����C������![]() ����A��B��������A�ڵ�B�����������A����B�ĺ�������һԪ���η���
����A��B��������A�ڵ�B�����������A����B�ĺ�������һԪ���η���![]() ����������
����������
��1�������A����B�����꼰�ö��κ�������ʽ��

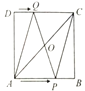
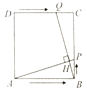
��2����ͼ2������AC��BC����Q���߶�OB��һ����������Q�����O��B�غ���������Q��QD��AC����BC��D����Q��������m��0��������CDQ���S���ʱ����m��ֵ��
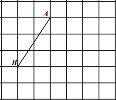
��3����ͼ3���߶�MN��ֱ��y=x�ϵĶ��߶�����M�ڵ�N���������MN=![]() ����M��ĺ�����Ϊn������M��x��Ĵ�����x�ύ�ڵ�P������N��x��Ĵ����������߽��ڵ�Q���Ե�P��M��Q��NΪ������ı����ܷ�Ϊƽ���ı��Σ������������n��ֵ������������˵��������
����M��ĺ�����Ϊn������M��x��Ĵ�����x�ύ�ڵ�P������N��x��Ĵ����������߽��ڵ�Q���Ե�P��M��Q��NΪ������ı����ܷ�Ϊƽ���ı��Σ������������n��ֵ������������˵��������
���𰸡���1��A����2��0����B��6��0����![]() ����2��
����2��![]() ����3��n=1��
����3��n=1��![]() ��-1��
��-1��![]() ��
��
�������������������1����һԪ���η���x2-4x-12=0����A��B�������ꣻ��A��B�������������κ���y=ax2+bx+6��������κ�������ʽ��
��2����DQ��AC����BDQ�ס�BCA���������Ʊȱ�ʾ��BDQ����������������������ʽ��ʾ��ACQ�����������S��CDQ=S��ABC-S��BDQ-S��ACQ�����ö��κ�����������������ʱ��m��ֵ��
��3���Ե�P��M��Q��NΪ������ı�����Ϊƽ���ı��Σ���ΪM��N��λ�ò�ȷ��������Ҫ������������ۣ�������������nֵ���ɣ�
�����������1����һԪ���η���x2-4x-12=0�����������ֱ���x=2��6����A����B�ĺ������Ƿ��̵�����������A�ڵ�B����࣬
��A��-2��0����B��6��0������A��B���������������y=ax2+bx+6����
![]() ��
��
���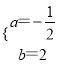 ��
��
��y=-![]() x2+2x+6��
x2+2x+6��
��2�������⣬��AB=8��QB=6-m��AQ=m+2��OC=6����S��ABC=![]() AB��OC=24��
AB��OC=24��
����DQ��AC��
���BDQ�ס�BCA��
��![]() ��
��
��S��BDQ=![]() ��m-6��2��
��m-6��2��
�֡�S��ACQ=![]() AQ��OC=3m+6��
AQ��OC=3m+6��
��S=S��ABC-S��BDQ-S��ACQ=24-![]() ��m-6��2-��3m+6��=-
��m-6��2-��3m+6��=-![]() m2+
m2+![]() m+
m+![]() =-
=-![]() ��m-2��2+6��
��m-2��2+6��
�൱m=2ʱ��S���
��3����MN=![]() ����A��B����ֱ��y=x�ϣ�MN��ֱ��AB�ϣ�MN���߶� AB�ϣ�M�ĺ�����Ϊn��������ҲΪn��
����A��B����ֱ��y=x�ϣ�MN��ֱ��AB�ϣ�MN���߶� AB�ϣ�M�ĺ�����Ϊn��������ҲΪn��
��ͼ3������M��x���ƽ���ߣ�����N��y���ƽ���ߣ������ཻ�ڵ�H��
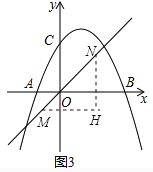
���MHN�ǵ���ֱ�������Σ�
��MH=NH=1��
���N��������n+1��n+1����
����ͼ4����n��0ʱ��PM=n��
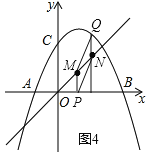
NQ=n+1-[-![]() ��n+1��2+2��n+1��+6]��
��n+1��2+2��n+1��+6]��
���ı���PMQNΪƽ���ı���ʱ��PM=NQ��
��n=n+1-[-![]() ��n+1��2+2��n+1��+6]��
��n+1��2+2��n+1��+6]��
���n=-1+![]() ��
��![]() -1��
-1��
����ͼ5����n��0ʱ��PM=-m��
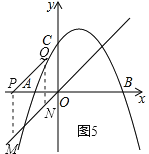
NQ=n+1-[-![]() ��n+1��2+2��n+1��+6]��
��n+1��2+2��n+1��+6]��
���ı���PMQNΪƽ���ı���ʱ��PM=NQ��
��-n=n+1-[-![]() ��n+1��2+2��n+1��+6]��
��n+1��2+2��n+1��+6]��
���n=1-![]() ��n=-1-
��n=-1-![]() ��
��
�ۡ�ֱ��AB��O����ֱ�߾�����һ�������ޣ�
���M�ڵ�3����N�ڵ�2�������ڣ�
���������Ե�P��M��Q��NΪ������ı�����Ϊƽ���ı��Σ�n��ֵ��n=1��![]() ����n=-1��
����n=-1��![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�