Question

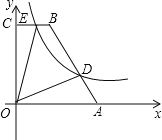
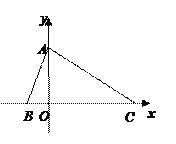
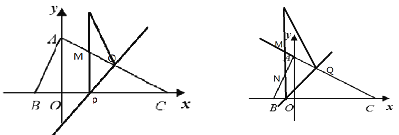
【题目】如图，在平面直角坐标系中，点A、B、C的坐标分别为（0，2）、（－1，0）、（4，0）．P是线段BC上的一动点（点P与点B、C不重合），假设p的横坐标是t.过点P的直线与直线y＝x平行且与AC相交于点Q．设△QPC关于直线PQ的对称的图形与四边形ABPQ重叠部分的面积为S．

⑴点C关于直线PQ的对称点C′的坐标为________；

⑵△ABC是什么三角形？为什么？

（3）求S与t的函数关系式．

Answer 1

【答案】（t,4-t）

【解析】试题分析： 画图可知，点C′的横坐标就是点的横坐标，纵坐标就是的长度.

根据坐标分别求出的长度，根据勾股定理的逆定理即可判定是直角三角形.

分类讨论即可.

试题解析：

是直角三角形.

由得

根据勾股定理得:

得

得是直角三角形.

（3）当时 直线的表达式是,直线的表达式是

设与直线交于 可得点坐标

点的坐标

当时设与直线交于

可得直线的表达式是,

得N坐标是

的面积是