题目内容
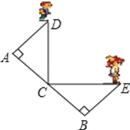
【题目】如图,已知∠ABC=120°,BD平分∠ABC,∠DAC=60°,若AB=2,BC=3,则BD的长是( )
A. 5 B. 7 C. 8 D. 9
【答案】A
【解析】
在CB的延长线上取点E,使BE=AB,连接AE,则可证得△ABE为等边三角形,再结合条件可证明△ABD≌△AEC,可得BD=CE,再利用线段的和差可求得CE,则可求得BD.
在CB的延长线上取点E,使BE=AB,连接AE,
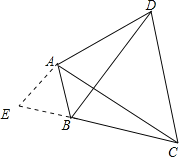
∵∠ABC=120,
∴∠ABE=180∠ABC=60,
∵BE=AB,
∴△ABE为等边三角形,
∴AE=AB,∠BAE=∠E=60,
∵∠DAC=60,
∴∠DAC=∠BAE,
∵∠BAD=∠BAC+∠DAC,∠EAC=∠BAC+∠BAE,
∴∠BAD=∠EAC,
∵BD平分∠ABC,
∴![]()
∴∠ABD=∠E,
在△ABD和△AEC中,
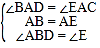
∴△ABD≌△AEC(ASA),
∴BD=CE,
∵CE=BE+BC=AB+BC=3+2=5,
∴BD=5,
故选:A.

练习册系列答案
相关题目