题目内容
【题目】AD是△ABC的高,AC=2 ![]() ,AD=4,把△ADC沿着直线AD对折,点C落在点E的位置,如果△ABE是等腰三角形,那么线段BE的长度为( )
,AD=4,把△ADC沿着直线AD对折,点C落在点E的位置,如果△ABE是等腰三角形,那么线段BE的长度为( )
A.2 ![]()
B.2 ![]() 或5
或5
C.2 ![]()
D.5
【答案】B
【解析】解:如图 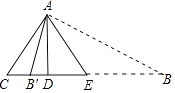
①当高AD在△ABC内时,由题意EA=EB=AC=2 ![]() .
.
②当高AD在△ACB′外时,设AB′=B′E=x.
在Rt△ADC中,CD= ![]() =
= ![]() =2,
=2,
由题意DE=DC=2,
在Rt△AED中,∵AB′2=AD2+DB′2 ,
∴x2=42+(x﹣2)2 ,
∴x=5.
∴线段BE的长度为2 ![]() 或5,
或5,
故选B.
【考点精析】本题主要考查了等腰三角形的性质和翻折变换(折叠问题)的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目