题目内容
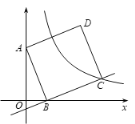
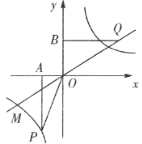
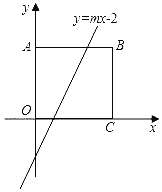
【题目】如图,在平面直角坐标系中,四边形ABCO是正方形,点B的坐标为(4,4).
(1)直线y=mx﹣2恰好把正方形ABCO的面积分成相等的两部分,则m=_____;
(2)若直线y=mx﹣2与正方形ABCO的边有两个公共点,则m的取值范围是_____.
【答案】2 m![]()
【解析】
(1)只有过正方形对角线交点的直线,才能把正方形分成面积相等的两部分.点B的坐标为(4,4),则y=mx﹣2经过点(2,2),代入直线解析式得m=2;
(2)根据题意得到C(4,0),把C(4,0)代入y=mx﹣2求得m=![]() ,于是得到结论.
,于是得到结论.
解:(1)∵直线y=mx﹣2恰好把正方形ABCO的面积分成相等的两部分,
∴直线必经过正方形的中心,
∵点B的坐标为(4,4),
∴中心为(2,2),代入直线中得:2=2m﹣2,m=2;
故答案为:2
(2)∵四边形ABCO是正方形,点B的坐标为(4,4),
∴C(4,0),
把C(4,0)代入y=mx﹣2得4m﹣2=0,
∴m=![]() ,
,
∴当m>![]() 时,直线y=mx﹣2与正方形ABCO的边有两个公共点,
时,直线y=mx﹣2与正方形ABCO的边有两个公共点,
故答案为:m>![]() .
.

【题目】某药品生产基地共有5条生产线,每条生产线每月生产药品20万盒,该基地打算从第一个月开始到第五个月结束,对每条生产线进行升级改造.改造时,每个月只升级改造一条生产线,这条生产线当月停产,并于下个月投入生产,其他生产线则正常生产.经调查,每条生产线升级改造后,每月的产量会比原来提高20%.
(1)根据题意,完成下面问题:
①把下表补充完整(直接写在横线上):
月数 | 第1个月 | 第2个月 | 第3个月 | 第4个月 | 第5个月 | 第6个月 | … |
产量/万盒 |
|
|
| 92 | … | … | … |
②从第1个月进行升级改造后,第 个月的产量开始超过未升级改造时的产量;
(2)若该基地第x个月(1≤x≤5,且x是整数)的产量为y万盒,求y关于x的函数关系式;
(3)已知每条生产线的升级改造费是30万元,每盒药品可获利3元.设从第1个月开始升级改造后,生产药品所获总利润为W1万元;同时期内,不升级改造所获总利润为W2万元设至少到第n个月(n为正整数)时,W1大于W2,求n的值.(利润=获利﹣改造费)