题目内容
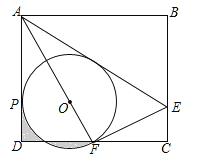
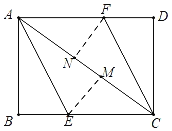
【题目】如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处,易证四边形AECF是平行四边形.当∠BAE为( )度时,四边形AECF是菱形.
A.30°B.40°C.45°D.50°
【答案】A
【解析】
由折叠性质得到∠BAE=∠CAE=30°,求得∠ACE=90°﹣30°﹣30°=60°,即∠CAE=∠ACE,得到EA=EC,于是得到结论.
解:当∠BAE=30°时,四边形AECF是菱形,
理由:由折叠可知,∠BAE=∠CAE=30°,
∵∠B=90°,
∴∠ACE=90°﹣30°﹣30°=30°,
即∠CAE=∠ACE,
∴EA=EC,
∵四边形AECF是平行四边形,
∴四边形AECF是菱形,
故选:A.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目