题目内容
【题目】四边形ABCD内接于⊙O， 
： 
： 
=2：3：5，∠BAD=120°，则∠ABC的度数为（ ）
A.100°
B.105°
C.120°
D.125°
【答案】B
【解析】解：如图所示：连接OA、OB、OC、OD，∵四边形ABCD为⊙O的内接四边形， 
： 
： 
=2：3：5，∠BAD=120°，
∴∠COD=150°，∠BOC=90°，∠AOB=60°，
∴∠AOD=60°，
∴∠ABC= 
（150°+60°）=105°；
故选：B．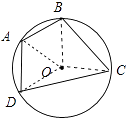
【考点精析】认真审题，首先需要了解圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半)，还要掌握圆内接四边形的性质(把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形)的相关知识才是答题的关键．
练习册系列答案
相关题目
