题目内容
【题目】如图,△ABC内接于⊙O,其外角平分线AD交⊙O于D,DM⊥AC于M,下列结论中正确的是
①DB=DC;
②AC+AB=2CM;
③AC﹣AB=2AM;
④S△ABD=S△ABC . 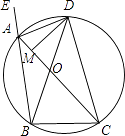
【答案】①②③
【解析】解:过点D作DF⊥BE于F,∵A、B、C、D四点共圆,
∴∠FAD=∠BCD,
∵外角平分线AD交⊙O于D,
∴∠FAD=∠DAC,
又∵∠DBC=∠DAC,
∴∠BCD=∠CBD,
∴①DB=DC,故此选项正确;
∵AD外角平分线,DF⊥BE,DM⊥AC于M,
∴DF=DM,
在△BFD≌△CMD中, ,
,
∴Rt△BFD≌Rt△CMD,
∴BF=CM,
又∵AF=AM,
∴②AC﹣AB=CM+AM﹣AB=CM+AM﹣CM+AF=CM+AM﹣CM+AM=2AM,故此选项正确;
∴③AC+AB=AM+MC+BF﹣FA=AM+MC+MC﹣AM=2CM,故此选项正确;
S△ABD和S△ABC的大小无法判断,④错误,
故答案为:①②③.
由A、B、C、D四点共圆,可得∠FAD=∠BCD,由同弧所对的圆周角相等得到圆周角相等,结合外角平分线可得∠BCD=∠CBD,可得BD=CD;过点D作DF⊥BE,可以通过证明三角形全等,通过边的关系可以得到②AC﹣AB=2AM,③AC+AB=2CM都是正确的;S△ABD和S△ABC的大小无法判断.

练习册系列答案
相关题目