Question

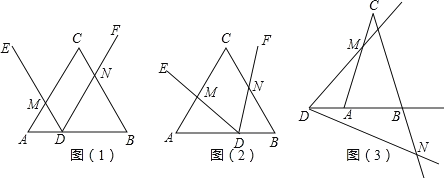
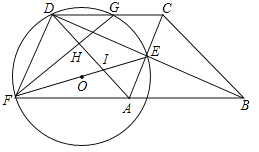
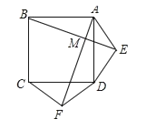
【题目】如图，在正方形ABCD的外侧， 作两个等腰三角形ADE和DCF，

(1) 若EA=ED=FD=FC，请判断BE和AF的关系？并给予证明．

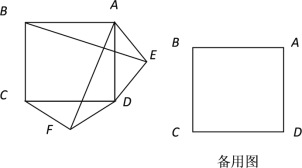
(2)若三角形ADE和DCF为一般三角形，且AE=DF，ED=FC，请用备用图画出图形，直接写出BE和AF的关系，不用证明．

Answer 1

【答案】（1）AF＝BE，AF⊥BE，理由见解析（2）AF＝BE，AF⊥BE，理由见解析

【解析】

（1）根据正方形的性质、等腰三角形的性质以及全等三角形的判定定理证明△BAE≌△ADF，根据全等三角形的性质进行证明；

（2）同（1）一样的方法证明即可．

（1）在正方形ABCD中，∠BAD＝∠ADC＝90，AB＝AD＝CD．

∵EA＝ED＝FD＝FC，

在△AED和△DFC中，

，

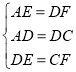∴△AED≌△DFC（SSS），

∴∠EAD＝∠FDC．

∴∠BAD＋∠EAD＝∠ADC＋∠FDC．

即∠BAE＝∠ADF．

在△BAE和△ADF中，

，

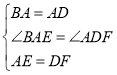∴△BAE≌△ADF（SAS）

∴AF＝BE，

∴∠ABE＝∠DAF．

∵∠DAF＋∠BAF＝90，

∴∠ABE＋∠BAF＝90，

∴∠AMB＝90，

∴AF⊥BE．

故AF＝BE，AF⊥BE．

（2）所画图形如图，AF＝BE，AF⊥BE理由如下：

在△AED和△DFC中，

，

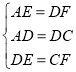∴△AED≌△DFC（SSS），

∴∠EAD＝∠FDC．

∴∠BAD＋∠EAD＝∠ADC＋∠FDC．即∠BAE＝∠ADF．

在△BAE和△ADF中， ，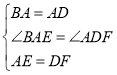

∴△BAE≌△ADF（SAS），

∴AF＝BE，

∴∠ABE＝∠DAF．

∵∠DAF＋∠BAF＝90，

∴∠ABE＋∠BAF＝90，

∴∠AMB＝90，

∴AF⊥BE．

故AF＝BE，AF⊥BE．