题目内容
【题目】如图,为测量江两岸码头B、D之间的距离,从山坡上高度为50米的A处测得码头B的俯角∠EAB为15°,码头D的俯角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求码头B、D的距离(结果保留整数).
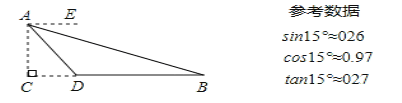
【答案】135米
【解析】解:∵AE∥BC,∴∠ADC=∠EAD=45°。
又∵AC⊥CD,∴CD=AC=50。
∵AE∥BC,∴∠ABC=∠EAB=15°。
又∵![]() , ∴
, ∴![]() 。
。
∴BD≈185.2﹣50≈135(米)。
答:码头B、D的距离约为135米。
由∠EAB=15°,根据平行的性质,可得∠ABC=∠EAB=15°。从而解直角三角形ABC可求得BC的长。由∠ADC=∠EAD=45°可得CD=AC=50。从而由BD=BC-CD可求得B、D的距离。

练习册系列答案
相关题目
【题目】七(一)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据整理如下表(部分):
月均用水量x/m3 | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 | x>20 |
频数/户 | 12 | 20 | 3 | ||
频率 | 0.12 | 0.07 |
若该小区有800户家庭,据此估计该小区月均用水量不超过10m3的家庭约有________户.