题目内容
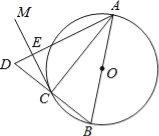
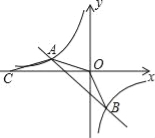
【题目】如图,直线AB与反比例函数的图象交于A(﹣4,m)、B(2,n)两点,点C在x轴上,AO=AC,△OAC的面积为8.
(1)求反比例函数的解析式.
(2)求cos∠OBA的值.
【答案】(1)y=﹣![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)因为△ACO是等腰三角形,根据三角形面积公式即可求出m,得点A坐标,用待定系数法可以求出反比例函数的解析式.(2)作OE⊥AB于E,欲求cos∠OBA,因为cos∠OBA=![]() ,只要求出OB、BE即可,利用两点间距离公式可求出OB、BE.
,只要求出OB、BE即可,利用两点间距离公式可求出OB、BE.
试题解析:(1)设反比例函数为y=![]() ,∵△OAC的面积为8,AO=AC,A(﹣4,m),∴点C(﹣8,0),
,∵△OAC的面积为8,AO=AC,A(﹣4,m),∴点C(﹣8,0),![]() 8m=8,∴m=2,∴点A(﹣4,2),∵反比例函数的图象经过A(﹣4,2)、B(2,n)两点,∴k=﹣8,n=﹣4,∴点B坐标(2,﹣4),∴反比例函数解析式为y=﹣
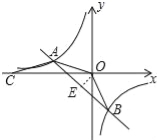
8m=8,∴m=2,∴点A(﹣4,2),∵反比例函数的图象经过A(﹣4,2)、B(2,n)两点,∴k=﹣8,n=﹣4,∴点B坐标(2,﹣4),∴反比例函数解析式为y=﹣![]() ;(2)如图作OE⊥AB于E,由(1)可利用勾股定理求得,OA=OB=2
;(2)如图作OE⊥AB于E,由(1)可利用勾股定理求得,OA=OB=2![]() ,AB=6
,AB=6![]() ,∵OA=OB,OE⊥AB,∴AE=EB=3
,∵OA=OB,OE⊥AB,∴AE=EB=3![]() ,∴cos∠OBA=
,∴cos∠OBA=![]() =
=![]() =
=![]() .
.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目