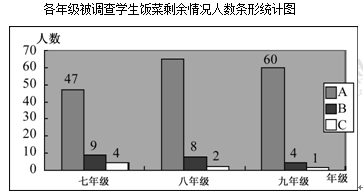
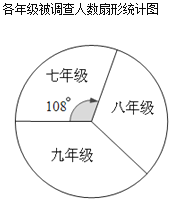
��Ŀ����
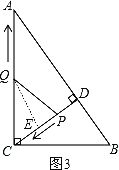
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AC=8��BC=6��CD��AB�ڵ�D����P�ӵ�D���������߶�DC���C�˶�����Q�ӵ�C���������߶�CA���A�˶�������ͬʱ�������ٶȶ�Ϊÿ��1����λ���ȣ�����P�˶���Cʱ�����㶼ֹͣ�����˶�ʱ��Ϊt����
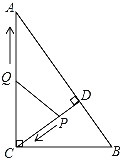
��1�����߶�CD�ij���
��2����tΪ��ֵʱ����CPQ����ABC���ƣ�
��3����tΪ��ֵʱ����CPQΪ���������Σ�
���𰸡���1��4��8����2��3��![]() ����3��2��4���
����3��2��4���![]() ���
���![]() ����
����
��������
�����������1���ȸ��ݹ��ɶ������AB�ij������������ε������ʽ���ɵó����ۣ�
��2������t��ʾ��DP��CQ��CP�ij����ٷ�PQ��CD��PQ��AC��������������ۣ�
��3���������⻭��ͼ�Σ���CQ=CP��PQ=PC��QC=QP�����������������
�����������1���ߡ�ACB=90�㣬AC=8��BC=6��
��AB=10��
��CD��AB��
��S��ABC=![]() BCAC=
BCAC=![]() ABCD��
ABCD��
��CD=![]() ��
��
���߶�CD�ij�Ϊ4��8��
��2�������֪���������Σ�
��DP=t��CQ=t����CP=4��8-t��
����PQ��CDʱ����ͼa
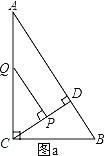
�ߡ�QCP�ס���ABC
��![]() ����
����![]() ��
��
��t=3��
����PQ��AC����ͼb��
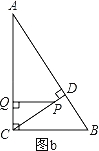
�ߡ�PCQ�ס�ABC
��![]() ����
����![]() �����t=
�����t=![]() ��
��
����tΪ3��![]() ʱ����CPQ������ABC���ƣ�
ʱ����CPQ������ABC���ƣ�
��3������CQ=CP����ͼ1��
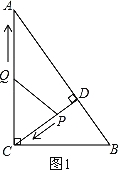
��t=4��8-t��
��ã�t=2��4��
����PQ=PC����ͼ2��ʾ��
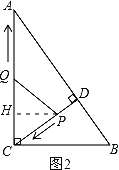
��PQ=PC��PH��QC��
��QH=CH=![]() QC=
QC=![]() ��
��
�ߡ�CHP�ס�BCA��
��![]() ��
��
��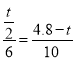 �����t=
�����t=![]() ��
��
����QC=QP��
����Q��QE��CP������ΪE����ͼ3��ʾ��
ͬ���ɵã�t=![]() ��
��
������������tΪ2��4���![]() ���
���![]() ��ʱ����CPQΪ������������
��ʱ����CPQΪ������������

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�