题目内容
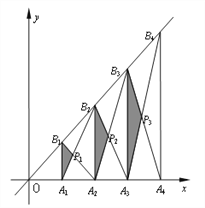
【题目】如图,已知A1、A2、……、An、An+1是x轴上的点,且OA1=A1A2=A2A3=……=AnAn+1=1,分别过点A1、A2、……、An、An+1作x轴的垂线交直线y=2x于点B1、B2、……、Bn、Bn+1,连接A1B2、B1A2、A2B3、B2A3、……、AnBn+1、BnAn+1,依次相交于点P1、P2、P3、……、Pn,△A1B1P1、△A2B2P2、……、△AnBnPn的面积依次为S1、S2、……、Sn,则Sn为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】试题分析:∵A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,
∴A1(1,0),
A2(2,0),
A3(3,0),
…
An(n,0),
An+1(n+1,0),
∵分别过点A1、A2、A3、…、An、An+1,作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,
∴B1的横坐标为:1,纵坐标为:2,
则B1(1,2),
同理可得:B2的横坐标为:2,纵坐标为:4,
则B2(2,4),
B3(2,6),
…
Bn(n,2n),
Bn+1(n+1,2n+2),
根据题意知:P n是AnBn+1与 BnAn+1的交点,
设:直线AnBn+1的解析式为:y=k1x+b1,
直线BnAn+1的解析式为:y=k2x+b2,
∵An(n,0),An+1(n+1,0),Bn(n,2n),Bn+1(n+1,2n+2),
∴直线AnBn+1的解析式为:y=(2n+2)x﹣2n2﹣2n,
直线BnAn+1的解析式为:y=﹣2n x+2n2+2n,
∴P n(![]() ,
, ![]() )
)
∴△AnBnPn的AnBn边上的高为: ![]() =
=![]() ,
,
△AnBnPn的面积Sn为: ![]() .
.
故选D.

练习册系列答案
相关题目