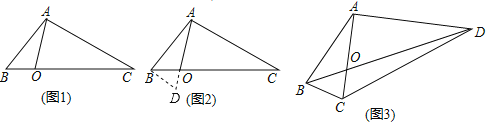
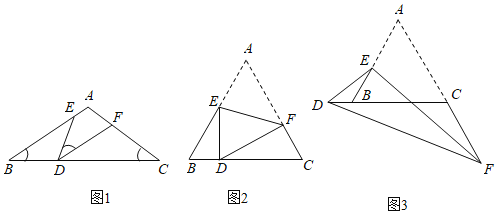
题目内容
【题目】如图,在![]() 中,已知
中,已知![]() ,
,![]() ,且
,且![]() ,将
,将![]() 与
与![]() 重合在一起,若
重合在一起,若![]() 位置保持不动,滑动
位置保持不动,滑动![]() ,且使点
,且使点![]() 在边
在边![]() 上沿
上沿![]() 到
到![]() 的方向运动,
的方向运动,![]() 始终经过点
始终经过点![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
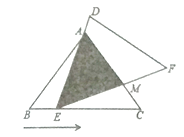
(1)若![]() ,求
,求![]() 的长;
的长;
(2)探究:当![]() 离开
离开![]() 后,
后,![]() 在其它运动过程中,重叠部分(即
在其它运动过程中,重叠部分(即![]() )能否构成等腰三角形?若能,求出
)能否构成等腰三角形?若能,求出![]() 的长;若不能,请说明理由.
的长;若不能,请说明理由.
【答案】(1) ![]() ;(2)能,当
;(2)能,当![]() 或
或![]() 时,重叠部分能构成等腰三角形.
时,重叠部分能构成等腰三角形.
【解析】
(1)根据题中条件先求证![]() ,再根据相似三角形的性质代已知线段的长,从而求出CM的长.
,再根据相似三角形的性质代已知线段的长,从而求出CM的长.
(2)由于![]() 为等腰三角形时哪两条边相等不明确,所以要分类讨论.根据等腰三角形的腰相等分三种情况讨论即可.
为等腰三角形时哪两条边相等不明确,所以要分类讨论.根据等腰三角形的腰相等分三种情况讨论即可.
解:(1)∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]()
∴![]()
∴![]()
∴![]()
(2)能.
①若![]() ,
,![]() 为等腰三角形,
为等腰三角形,
因为![]() ,
,![]() ,
,![]()
所以![]() ,
,![]()
所以![]() ,
,![]()
②若![]() ,
,![]() 为等腰三角形,则有
为等腰三角形,则有![]()
∴![]() ,即
,即![]()
又∵![]() ,
,
∴![]() ,
,
∴![]()
∴![]() .
.
∴![]()
③∵![]() 又
又
∵![]()
∴![]()
∴![]() .
.
综上所述,当![]() 或
或![]() 时,重叠部分能构成等腰三角形.
时,重叠部分能构成等腰三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目