题目内容
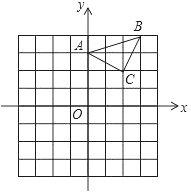
【题目】在平面直角坐标系中，已知点A（1，2）和点B（4，5），当直线y＝kx﹣2k（k为常数）与线段AB有交点时，k的取值范围为（ ）
A.k≤﹣2或k≥
B.﹣2≤k≤
C.﹣2≤k≤0或0≤k≤D.﹣2＜k＜0或0＜k＜
【答案】A
【解析】
直线y＝kx﹣2k（k为常数）恒过点P（2，0）,分别把点A（1，2）和点B（4，5）代入解析式即可求得k1和k2，要使直线y＝kx﹣2k（k为常数）与线段AB有交点，继而根据一次函数的性质即可求得答案.
解：∵y＝kx﹣2k＝k（x﹣2）
∴直线y＝kx﹣2k（k为常数）恒过点P（2，0）
当直线刚好过点A时，将A（1，2）代入y＝kx﹣2k中得：
kPA＝﹣2，
当直线刚好过点B时，将B（4，5）代入y＝kx﹣2k中得：
kPB＝
，
∴当直线y＝kx﹣2k（k为常数）与线段AB有交点时，k的取值范围为：k≤﹣2或k≥，
故选：A．
练习册系列答案
黄冈创优卷系列答案
相关题目
