��Ŀ����
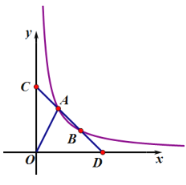
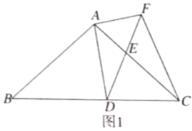
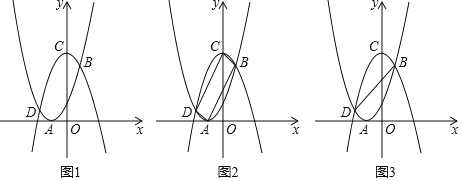
����Ŀ����ͼ��ʾ�������κ���y=x2+2x+1��ͼ����x�ᷭ�ۣ�Ȼ������ƽ��1����λ��������ƽ��5����λ���õ����κ���y=ax2+bx+c��ͼ����y=x2+2x+1��ͼ��Ķ���Ϊ��A������y=ax2+bx+c��ͼ��Ķ���Ϊ��C��������ͼ��ֱ���B��D���㣮
��1������y=ax2+bx+c�Ľ���ʽ��
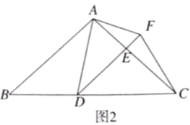
��2����ͼ2������AD��CD��BC��AB���ж��ı���ABCD����״����˵�����ɣ�
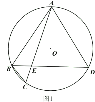
��3����ͼ3������BD����M��y���ϵĶ��㣬��ƽ�����Ƿ����һ��N��ʹ��B��D��M��NΪ������ı���Ϊ���Σ������ڣ������N������ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=��x2+5����2���ı���ABCD��ƽ���ı��Σ����ɼ���������3�����ڣ���N����Ϊ(![]() ��
��![]() )��(
)��(![]() ��
��![]() )��(3��2)��(��3��2)��
)��(3��2)��(��3��2)��
��������
(1)����Գƺ�ƽ�Ƶ����ʿ���⣻
(2)�ֱ������A����B����C����D���꣬��������빫ʽ����AB��CD��AD��BC��AC��BD�ij���������Ա���ȵ��ı�����ƽ���ı��ο�֤�ı���ABCD��ƽ���ı��Σ�
(3)������������ۣ����þ��ε����ʣ�����⣮
(1)��y=x2+2x+1=(x+1)2���ҽ����κ���y=x2+2x+1��ͼ����x�ᷭ�ۣ�Ȼ������ƽ��1����λ��������ƽ��5����λ��
��y=��(x+1��1)2+5=��x2+5��
(2)�ı���ABCD��ƽ���ı��Σ��������£�
��y=��x2+5�Ķ���Ϊ��C��
���C������Ϊ(0��5)��
�ߺ���y=x2+2x+1��ͼ��Ķ���Ϊ��A��
���A(��1��0)��
����������ɵã� ��
��
�� ![]() ��
�� ![]() ��
��
���D������Ϊ(��2��1)����B������Ϊ(1��4)��
�ߵ�D(��2��1)����B(1��4)����A(��1��0)����C(0��5)��
��![]() ��
��
ͬ������ã�CD=![]() ��AD=
��AD=![]() ��BC=
��BC=![]() ��AC=
��AC=![]() ��BD=3
��BD=3![]() ��
��
��AB=CD��AD=BC��
���ı���ABCD��ƽ���ı��Σ�
(3)���ڣ�
���N(x��y)
��BDΪ���εıߣ��ı���BDMN�Ǿ���ʱ��

�ߵ�D������Ϊ(��2��1)����B������Ϊ(1��4)��
��ֱ��BD����ʽΪ��![]() ��
��
��![]() ��
��
��ã�![]() ��
��
��ֱ��BD����ʽΪ��y=x+3��
��DM��BD��
����ֱ��DM�Ľ���ʽΪ![]() ��
��
����D������Ϊ(��2��1)����ã�![]() ��
��
��ã�![]() ��
��
��ֱ��DM�Ľ���ʽΪy=��x��1��
���M������Ϊ(0����1)��
��BM��DN����ƽ�֣�
��![]() ��
��![]() ��
��
��x=3��y=2��
���N������Ϊ(3��2)��
��BDΪ���εıߣ��ı���BDNM�Ǿ���ʱ��

�ߵ�D������Ϊ(��2��1)����B������Ϊ(1��4)��ֱ��BD����ʽΪ��y=x+3��
��BM��BD��
����ֱ��BM�Ľ���ʽΪ![]() ��
��
����B������Ϊ(1��4)����ã�![]() ��
��
��ã�![]() ��
��
��ֱ��BM�Ľ���ʽΪy=��x+5��
���M������Ϊ(0��5)��
��BN��DM����ƽ�֣�
��![]() ��
��![]() ��
��
��x=��3��y=2��
���N������Ϊ(��3��2)��
��BDΪ�Խ��ߣ�
�ߵ�D��B��N������ֱ�Ϊ(��2��1)�� (1��4)�� (x��y)��
��M�ĺ�����Ϊ0�����M��������Ϊ![]() ��
��

��BD��MN����ƽ�֣�
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��N������Ϊ(![]() ��
��![]() )����M������Ϊ(0��5��y)��
)����M������Ϊ(0��5��y)��
��BD=MN��
��![]()
�����ã�![]()
��ã�![]() ��
��
���N������Ϊ(![]() ��
��![]() )��(
)��(![]() ��
��![]() )��
)��
������������N����Ϊ(![]() ��
��![]() )��(
)��(![]() ��
��![]() )��(3��2)��(��3��2)��
)��(3��2)��(��3��2)��