题目内容
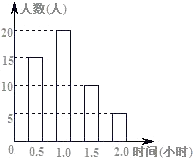
【题目】如图,直线y=x﹣1与反比例函数y= ![]() 的图象交于A,B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
的图象交于A,B两点,与x轴交于点C,已知点A的坐标为(﹣1,m). 
(1)反比例函数的解析式为 , 直线y=x﹣1在双曲线y= ![]() 上方时x的取值范围是;
上方时x的取值范围是;
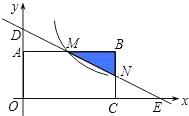
(2)若点P(n,﹣1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.
【答案】
(1)y= ![]() ;﹣1<x<0或x>2
;﹣1<x<0或x>2
(2)解:∵点P(n,﹣1)是反比例函数图象上一点,
∴﹣1= ![]() ,解得n=﹣2,
,解得n=﹣2,
∴E(﹣2,0),F(﹣2,﹣3).
∵直线y=x﹣1中,当x=0时,x=1,
∴C(1,0),
∴CE=|﹣2﹣1|=3,
∴S△CEF= ![]() CEEF=
CEEF= ![]() ×3×3=
×3×3= ![]()
【解析】解:(1)∵A(﹣1,m),
∴m=﹣1﹣1=﹣2,
∴A(﹣1,﹣2),
∴k=(﹣1)×(﹣2)=2,
∴反比例函数的解析式为y= ![]() .
.
联立一次函数与反比例函数的解析式得 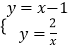 ,解得
,解得 ![]() 或
或 ![]() ,
,
∴B(2,1).
由函数图象可知,当﹣1<x<0或x>2时,直线y=x﹣1在双曲线y= ![]() 上方.
上方.
所以答案是:y= ![]() ,﹣1<x<0或x>2;
,﹣1<x<0或x>2;

练习册系列答案
相关题目
【题目】某水果公司购进10 000kg苹果,公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计,部分结果如下表:
苹果总质量n(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
损坏苹果质量m(kg) | 10.50 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
苹果损坏的频率 (结果保留小数点后三位) | 0.105 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
估计这批苹果损坏的概率为_____(结果保留小数点后一位),损坏的苹果约有______kg.