题目内容
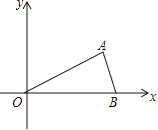
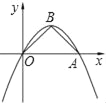
【题目】如图，抛物线y＝ax2+bx经过点A（4，0）、B（2，2），连接OB、AB．
（1）求抛物线的解析式；
（2）求证：△OAB是等腰直角三角形．
【答案】（1）抛物线的解析式为：y＝﹣
x2+2x；（2）证明见解析.
【解析】
（1）将A、B的坐标代入抛物线的解析式中，通过联立方程组即可求出抛物线的解析式；
（2）过B作BC⊥x轴于C，根据A、B的坐标易求得OC=BC=AC=2，由此可证得∠BOC、∠BAC、∠OBC、∠ABC都是45°，即可证得△OAB是等腰直角三角形.
（1）解：由题意得
，
解得
；
∴该抛物线的解析式为：y＝﹣
x2+2x；
（2）证明：过点B作BC⊥x轴于点C，则OC＝BC＝AC＝2；
∴∠BOC＝∠OBC＝∠BAC＝∠ABC＝45°；
∴∠OBA＝90°，OB＝AB；
∴△OAB是等腰直角三角形；
练习册系列答案
相关题目
【题目】某射击教练为了了解队员训练情况，从队员中选取甲、乙两名队员进行射击测试，相同条件下各射靶5次，成绩统计如下：
命中环数 | 6 | 7 | 8 | 9 | 10 |
甲命中相应环数的次数 | 0 | 1 | 3 | 1 | 0 |
乙命中相应环数的次数 | 2 | 0 | 0 | 2 | 1 |
（1）试通过计算说明甲、乙两人的成绩谁比较稳定？
（3）如果乙再射击1次，命中8环，那么乙射击成绩的方差会 ．（填“变大”、“变小”或“不变”）
