题目内容
【题目】如图,点B,F,C,E在一条直线上,AB=DE,AB∥DE,∠A=∠D.
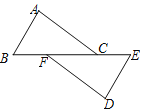
(1)求证:△ABC≌△DEF;(2)AC和DF存在怎样的关系?(直接写出答案)
【答案】(1)证明见解析;(2)AC=DF,AC∥DF.
【解析】
(1)根据两直线平行,内错角相等可得∠B=∠E,然后利用“角边角”证明△ABC和△DEF全等即可;
(2)根据全等三角形对应边相等可得AC=DF,对应角相等可得∠ACB=∠DFE,再利用内错角相等,两直线平行证明即可.
(1)∵AB∥DE,∴∠B=∠E.在△ABC和△DEF中,∵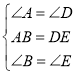 ,∴△ABC≌△DEF(ASA);
,∴△ABC≌△DEF(ASA);
(2)AC=DF,AC∥DF.理由如下:
∵△ABC≌△DEF,∴AC=DF,∠ACB=∠DFE,∴AC∥DF.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目