题目内容
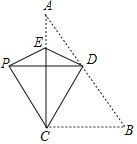
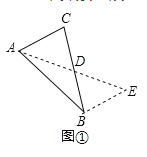
【题目】已知等边![]() 边长为8cm,点
边长为8cm,点![]() 是
是![]() 的中点,点
的中点,点![]() 在射线
在射线![]() 上运动,以
上运动,以![]() 为边在
为边在![]() 右侧作等边
右侧作等边![]() ,作射线
,作射线![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() .
.

(1)当点![]() 在线段
在线段![]() (不包括端点
(不包括端点![]() )上时,求证:
)上时,求证:![]() ;
;
(2)求证:![]() 平分
平分![]() ;
;
(3)连接![]() ,点
,点![]() 在移动过程中,线段
在移动过程中,线段![]() 长的最小值等于 (直接写出结果)
长的最小值等于 (直接写出结果)
【答案】(1)见解析;(2)见解析;(3)DF最小值为2cm.
【解析】
(1)欲证明BE=CF,只要证明△BAE≌△CAF(SAS)即可;
(2)首先证明∠BCM=90°,然后可得∠AMD=∠CMD=60°,求出∠AMN=60°即可;
(3)作DH⊥CN于H,根据点F的运动轨迹是射线CN可知,当点F与H重合时,DF的长最小,然后利用含30°直角三角形的性质求出DH即可.
(1)证明:∵△ABC,△AEF都是等边三角形,
∴AB=AC,AE=AF,∠BAC=∠EAF,
∴∠BAE=∠CAF,
∴△BAE≌△CAF(SAS),
∴BE=CF;
(2)证明:∵△ABC是等边三角形,AD=DC,
∴BD⊥AC,∠ACB=∠ABC=∠BAC=60°,
∴∠ABE=∠CBE=30°,MA=MC,
∵△BAE≌△CAF,
∴∠ABE=∠ACF=30°,
∴∠BCM=90°,
∴∠BMC=90°﹣30°=60°,
∵MA=MC,MB⊥AC,
∴∠AMD=∠CMD=60°,
∴∠AMN=60°,
∴∠AMN=∠AMD,
∴AM平分∠BMN.
(3)解:如图,作DH⊥CN于H.
∵∠BCN=90°,
∴点F的运动轨迹是射线CN,
根据垂线段最短可知,当点F与H重合时,DF的长最小,
∵CD=AD=4cm,∠DCH=30°,∠DHC=90°,
∴DH=![]() CD=2cm,
CD=2cm,
∴DF最小值为2cm.
故答案为2cm.


练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目