题目内容
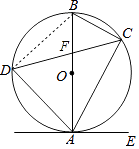
【题目】如图,已知AB是⊙O的直径,弦CD与直径AB相交于点F.点E在⊙O外,做直线AE,且∠EAC=∠D 
(1)求证:直线AE是⊙O的切线.
(2)若∠BAC=30°,BC=4,cos∠BAD= ![]() ,CF=
,CF= ![]() ,求BF的长.
,求BF的长.
【答案】
(1)证明:连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
即∠ADC+∠CDB=90°,
∵∠EAC=∠ADC,∠CDB=∠BAC,
∴∠EAC+∠BAC=90°,
即∠BAE=90°,
∴直线AE是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
Rt△ACB中,∠BAC=30°,
∴AB=2BC=2×4=8,
由勾股定理得:AC= ![]() =4
=4 ![]() ,
,
Rt△ADB中,cos∠BAD= ![]() =
= ![]() ,
,
∴ ![]() ,
,
∴AD=6,
∴BD= ![]() =2
=2 ![]() ,
,
∵∠BDC=∠BAC,∠DFB=∠AFC,
∴△DFB∽△AFC,
∴ ![]() ,
,
∴ ![]() ,
,
∴BF= ![]() .
.
【解析】(1)由直径所对的圆周角是直角得:∠ADB=90°,则∠ADC+∠CDB=90°,所以∠EAC+∠BAC=90°,则直线AE是⊙O的切线;(2)分别计算AC和BD的长,证明△DFB∽△AFC,列比例式得: ![]() ,得出结论.
,得出结论.
【考点精析】利用解直角三角形对题目进行判断即可得到答案,需要熟知解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目