题目内容
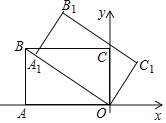
【题目】如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn﹣1Bn都为等腰直角三角形(点B0是坐标原点),则△A2014B2013B2014腰长等于_____.

【答案】2014![]()
【解析】
利用等腰直角三角形的性质及点的坐标的关系求出第一个等腰直角三角形的腰长,用类似的方法求出第二个,第三个…的腰长,观察其规律,最后得出结果.
解:作A1C⊥y轴,A2E⊥y轴,垂足分别为C、E,
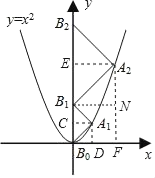
∵△A1B0B1、△A2B1B2都是等腰直角三角形,
∴B1C=B0C=DB0=A1D,B2E=B1E,
设A1(a,a),
将点A1的坐标代入解析式y=x2得:a=a2,
解得:a=0(不符合题意)或a=1,由勾股定理得:A1B0=![]() ,
,
则B1B0=2,
过B1作B1N⊥A2F,设点A2(x2,y2),
可得A2N=y2﹣2,B1N=x2=y2﹣2,
又点A2在抛物线上,所以y2=x22,即(x2+2)=x22,
解得x2=2,x2=﹣1(不合题意舍去),
则A2B1=2![]() ,同理可得:A3B2=3
,同理可得:A3B2=3![]() ,A4B3=4
,A4B3=4![]() …
…
∴A2014B2013=2014![]() ,
,
∴△A2014B2013B2014的腰长为:2014![]() .
.
故答案为:2014![]() .
.

【题目】为提升学生的艺术素养,某校计划开设四门选修课程:声乐、舞蹈、书法、摄影.要求每名学生必须选修且只能选修一门课程,为保证计划的有效实施,学校随机对部分学生进行了一次调查,并将调査结果绘制成如下不完整的统计表和统计图.
学生选修课程统计表
课程 | 人数 | 所占百分比 |
声乐 | 14 |
|
舞蹈 | 8 |
|
书法 | 16 |
|
摄影 |
|
|
合计 |
|
|

根据以上信息,解答下列问题:
(1)![]() ,
,![]() .
.
(2)求出![]() 的值并补全条形统计图.
的值并补全条形统计图.
(3)该校有1500名学生,请你估计选修“声乐”课程的学生有多少名.
(4)七(1)班和七(2)班各有2人选修“舞蹈”课程且有舞蹈基础,学校准备从这4人中随机抽取2人编排“舞蹈”在开班仪式上表演,请用列表法或画树状图的方法求所抽取的2人恰好来自同一个班级的概率.