题目内容
如图,线段AB的端点在边长为1的小正方形网格的格点上,现将线段AB绕点A按逆时针方 向旋转90°得到线段AC.
向旋转90°得到线段AC.
(1)请你在所给的网格中画出线段AC及点B经过的路径;
(2)若将此网格放在一平面直角坐标系中,已知点A的坐标为(1,3),点B的坐标为(-2,-1),则点C的坐标为______;
(3)线段AB在旋转到线段AC的过程中,线段AB扫过的区域记为图形T,若将图形T围成一个几何体的侧面,求该几何体底面圆的半径长.
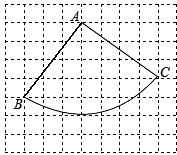 解:(1)如图;
解:(1)如图;(2)C的坐标为(5,0);

(3)l=
 =
=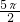 ,
,设该几何体底面圆的半径r,则2πr=
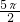 ,
,解得r=
 ,
,该几何体底面圆的半径长为
 .
.分析:(1)由旋转的性质可画出线段AC,点B经过的路径是以点A为圆心,AB长为半径的弧;
(2)根据点AB的坐标建立直角坐标系,从而得出点C的坐标;
(3)线段AB扫过的图形为扇形,它所围成的几何体为圆锥,可计算出圆锥的底面周长,从而求得底面半径.
点评:本题考查了扇形面积的计算、坐标与图形的性质,以及圆锥的计算,解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:
(1)圆锥的母线长等于侧面展开图的扇形半径;
(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.

练习册系列答案
相关题目
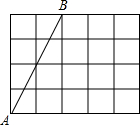 如图,线段AB的端点是4×5的正方形网格的格点,若再在网格的格点中取一点C,使△ABC成为等腰三角形,则符合条件的点C的个数是( )
如图,线段AB的端点是4×5的正方形网格的格点,若再在网格的格点中取一点C,使△ABC成为等腰三角形,则符合条件的点C的个数是( )| A、1个 | B、2个 | C、3个 | D、4个 |
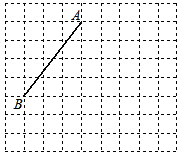 向旋转90°得到线段AC.
向旋转90°得到线段AC.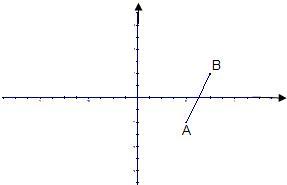 33、如图,线段AB的端点坐标为A(2,-1),B(3,1).试画出AB向左平移4个单位长度的图形,写出A、B对应点C、D的坐标,并判断A、B、C、D四点组成的四边形的形状.(不必说明理由).
33、如图,线段AB的端点坐标为A(2,-1),B(3,1).试画出AB向左平移4个单位长度的图形,写出A、B对应点C、D的坐标,并判断A、B、C、D四点组成的四边形的形状.(不必说明理由).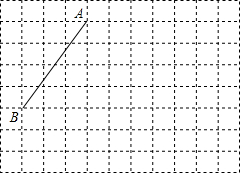 如图:线段AB的端点在边长为1的小正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.
如图:线段AB的端点在边长为1的小正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC. (2010•金东区模拟)如图,线段AB的端点在边长为1的小正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°.得到线段AC.
(2010•金东区模拟)如图,线段AB的端点在边长为1的小正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°.得到线段AC.