题目内容
【题目】如图,在平面直角坐标系中,直线![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像分别交于点A(2,m)、B(-4,-1),其中
的图像分别交于点A(2,m)、B(-4,-1),其中![]()
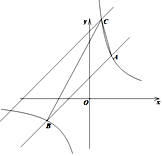
(1)求m的值和直线的解析式;
(2)若![]() ,观察图像,请直接写出x的取值范围;
,观察图像,请直接写出x的取值范围;
(3)将直线![]() 的图像向上平移与反比例函数的图像在第一象限内交于点C,C点的横坐标为1,
的图像向上平移与反比例函数的图像在第一象限内交于点C,C点的横坐标为1,
①判定△ABC的形状并说明理由,②求△ABC的面积.
【答案】(1)m=2, y1=![]() x1+1.;(2)-4<x<0或x>2 ;(3) ①直角三角形,理由见详解; ②
x1+1.;(2)-4<x<0或x>2 ;(3) ①直角三角形,理由见详解; ②![]()
【解析】
解:(1)根据题意得2m=-4×(-1),m=2,把A(2,m)和B(-4,-1)代入y1=kx1+b得到2=2k+b ;-1=-4k+b解得k、 b的值.因此求出直线AB 的解析式.
(2)根据直线在双曲线上部分所有的点的横坐标,既可得到x的取值范围.
(3)根据线段两点间的距离公式,求出AB、AC、BC的长,然后根据勾股定理逆定理解出三角形ΔABC是直角三角形,最后根据直角三角形面积公式求出该三角形的面积.
解:(1)根据题意得2m=-4×(-1),m=2,把A(2,2)和B(-4,-1)代入y1=kx1+b得到2=2k+b ;-1=-4k+b解得k=![]() b=1.所以y1=
b=1.所以y1=![]() x1+1.
x1+1.
(2)-4<x<0或x>2
(3)①A(2,2) B(-4,-1) C(1,4)所以AB=![]() ;AC=
;AC=![]() ;BC=
;BC=![]() , 因为AB2+AC2=BC2
, 因为AB2+AC2=BC2
即![]() 2+
2+![]() 2=
2=![]() 2所以ΔABC是直角三角形.
2所以ΔABC是直角三角形.
②由①知ΔABC是直角三角形AB=![]() ;AC=
;AC=![]() ,
,
SΔABC= =![]() ×
×![]() ×
×![]() =
=![]() .
.

【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?
【题目】我国是水资源比较贫乏的国家之一,为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段来达到节约用水的目的,规定如下用水收费标准:每户每月的用水不超过20立方米(含20立方米)时,水费按“基本价”收费:超过20立方米时,不超过的部分仍按“基本价”收费,超过部分按“调节价”收费.某户居民今年4、5月份的用水量和水费如下表所示:
月份 | 用水量(立方米) | 水费(元) |
4 | 20 | 42 |
5 | 24 | 56.40 |
(1)请你算一算该市水费的“调节价”每立方米多少元?
(2)若该户居民6月份用水量为30立方米,请算一算,6月份水费是多少元?