题目内容
【题目】△ABC是等边三角形,点D、E分别在边AB、BC上,CD、AE交于点F,∠AFD=60°.
(1)如图1,求证:BD=CE; 
(2)如图2,FG为△AFC的角平分线,点H在FG的延长线上,HG=CD,连接HA、HC,求证:∠AHC=60°; 
(3)在(2)的条件下,若AD=2BD,FH=9,求AF长.
【答案】
(1)解:如图1,
∵△ABC是等边三角形,
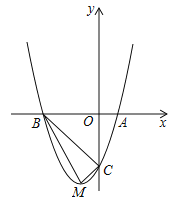
∴∠B=∠ACE=60°BC=AC,
∵∠AFD=∠CAE+∠ACD=60°∠BCD+∠ACD=∠ACB=60°,
∴∠BCD=∠CAE,
在△ABE和△BCD中,
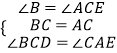
∴△ABE≌△BCD(ASA),
∴BD=CE;
(2)解:如图2,作CM⊥AE交AE的延长线于M,作CN⊥HF于N,

∵∠EFC=∠AFD=60°
∴∠AFC=120°,
∵FG为△AFC的角平分线,
∴∠CFH=∠AFH=60°,
∴∠CFH=∠CFE=60°,
∵CM⊥AE,CN⊥HF,
∴CM=CN,
∵∠CEM=∠ACE+∠CAE=60°+∠CAE,∠CGN=∠AFH+∠CAE=60°+∠CAE,
∴∠CEM=∠CGN,
在△ECM和△GCN中
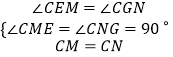
∴△ECM≌△GCN(AAS),
∴CE=CG,EM=GN,∠ECM=∠GCN,
∴∠MCN=∠ECG=60°,
∵△ABE≌△BCD,
∵AE=CD,
∵HG=CD,
∴AE=HG,
∴AE+EM=HG+GN,即AM=HN,
在△AMC和△HNC中
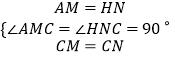
∴△AMC≌△HNC(SAS),
∴∠ACM=∠HCN,AC=HC,
∴∠ACM﹣∠ECM=∠HCN﹣∠GCN,即∠ACE=∠HCG=60°,
∴△ACH是等边三角形,
∴∠AHC=60°;
(3)解:如图3,在FH上截取FK=FC,
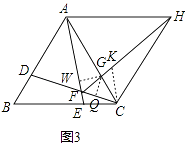
∵∠HFC=60°,
∴△FCK是等边三角形,
∴∠FKC=60°,FC=KC=FK,
∵∠ACH=60°,
∴∠ACF=∠HCK,
在△AFC和△HKC中
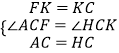
∴△AFC≌△HKC(SAS),
∴AF=HK,
∴HF=AF+FC=9,
∵AD=2BD,BD=CE=CG,AB=AC,
∴AG=2CG,
∴ ![]() =
= ![]() =
= ![]() ,
,
作GW⊥AE于W,GQ⊥DC于Q,
∵FG为△AFC的角平分线,
∴GW=GQ,
∵ ![]() =
= 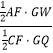 =
= ![]() =
= ![]() ,
,
∴AF=2CF,
∴AF=6.
【解析】(1)根据等边三角形的性质得出AB=BC,∠BAC=∠C=∠ABE=60°,根据SAS推出△ABE≌△BCD,即可证得结论;(2)根据角平分线的性质定理证得CM=CN,利用∠CEM=∠ACE+∠CAE=60°+∠CAE,∠CGN=∠AFH+∠CAE=60°+∠CAE,得出∠CEM=∠CGN,然后根据AAS证得△ECM≌△GCN,得出CG=CE,EM=GN,∠ECM=∠GCN,进而证得△AMC≌△HNC,得出∠ACM=∠HCN,AC=HC,从而证得△ACH是等边三角形,证得∠AHC=60°;(3)在FH上截取FK=FC,得出△FCK是等边三角形,进一步得出FC=KC=FK,∠ACF=∠HCK,证得△AFC≌△HKC得出AF=HK,从而得到HF=AF+FC=9,由AD=2BD可知AG=2CG,再由 ![]() =
= ![]() ,根据等高三角形面积比等于底的比得出
,根据等高三角形面积比等于底的比得出 ![]() =
= 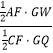 =
= ![]() =2,再由AF+FC=9求得.
=2,再由AF+FC=9求得.
【考点精析】关于本题考查的等边三角形的性质,需要了解等边三角形的三个角都相等并且每个角都是60°才能得出正确答案.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案