Question

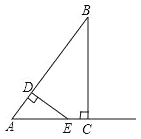
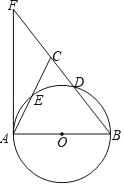
【题目】如图，AB是⊙O的直径，D是⊙O上一点，点E是AC的中点，过点A作⊙O的切线交BD的延长线于点F．连接AE并延长交BF于点C．

（1）求证：AB=BC；

（2）如果AB=5，tan∠FAC=，求FC的长．

Answer 1

【答案】(1)见解析;(2).

【解析】分析：（1）由AB是直径可得BE⊥AC，点E为AC的中点，可知BE垂直平分线段AC，从而结论可证；

（2）由∠FAC+∠CAB=90°，∠CAB+∠ABE=90°，可得∠FAC=∠ABE，从而可设AE=x，BE=2x，由勾股定理求出AE、BE、AC的长. 作CH⊥AF于H，可证Rt△ACH∽Rt△BAC，列比例式求出HC、AH的值，再根据平行线分线段成比例求出FH，然后利用勾股定理求出FC的值.

详解：（1）证明：连接BE.

∵AB是⊙O的直径，

∴∠AEB=90°，

∴BE⊥AC，

而点E为AC的中点，

∴BE垂直平分AC，

∴BA=BC；

（2）解：∵AF为切线，

∴AF⊥AB，

∵∠FAC+∠CAB=90°，∠CAB+∠ABE=90°，

∴∠FAC=∠ABE，

∴tan∠ABE=∠FAC=，

在Rt△ABE中，tan∠ABE==，

设AE=x，则BE=2x，

∴AB=x，即x=5，解得x=，

∴AC=2AE=2，BE=2

作CH⊥AF于H，如图，

∵∠HAC=∠ABE，

∴Rt△ACH∽Rt△BAC，

∴==，即==，

∴HC=2，AH=4，

∵HC∥AB，

∴=，即=，解得FH=

在Rt△FHC中，FC==．