Question

【题目】两张矩形纸片ABCD和CEFG完全相同，且AB=CE，AD＞AB．

操作发现：

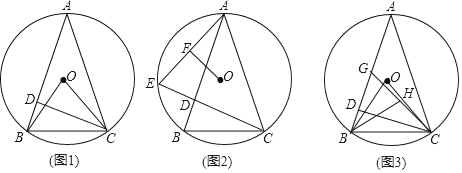
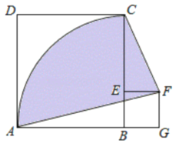
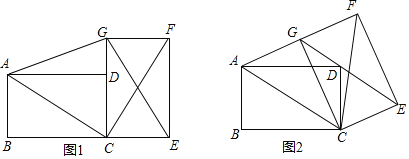
（1）如图1，点D在GC上，连接AC、CF、CG、AG，则AC和CF有何数量关系和位置关系？并说明理由．

实践探究：

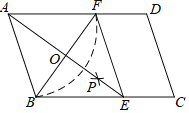
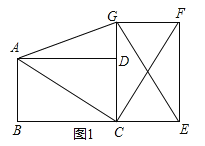
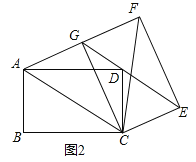
（2）如图2，将图1中的纸片CEFG以点C为旋转中心逆时针旋转，当点D落在GE上时停止旋转，则AG和GF在同一条直线上吗？请判断，并说明理由．

Answer 1

【答案】(1)；(2)，理由见解析.

【解析】

（1）先根据条件判定△ABC≌△CEF，进而得到AC=CF，∠ACB=∠CFE，再根据∠CFE+∠ECF=90°，得出∠ACF=90°，即可得到AC⊥CF；

（2）先根据条件判定△ACD≌△GEC，即可得出∠ACD=∠GEC，DC=EC，AC=GE，进而判定四边形ACEG是平行四边形，得出AG∥CE，再根据矩形CEFG中，GF∥CE，即可得到AG和GF在同一条直线上．

（1）AC=CF，AC⊥CF．理由如下：

如图1，

∵矩形纸片ABCD和CEFG完全相同，且AB=CE，

∴BC=EF，∠B=∠CEF=90°，

在△ABC和△CEF中，

，

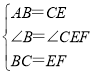∴△ABC≌△CEF（SAS），

∴AC=CF，∠ACB=∠CFE，

∵Rt△CEF中，∠CFE+∠ECF=90°，

∴∠ACB+∠ECF=90°，

∴∠ACF=∠BCD+∠ECG-（∠ACB+∠ECF）=90°+90°-90°=90°，

∴AC⊥CF；

（2）AG和GF在同一条直线上．理由如下：

如图2，

∵矩形纸片ABCD和CEFG完全相同，且AB=CE，

∴AD=GC，CD=CE，∠ADC=∠GCE=90°，

在△ACD和△GEC中，

，

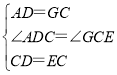∴△ACD≌△GEC（SAS），

∴∠ACD=∠GEC，DC=EC，AC=GE，

∴∠CDE=∠DEC，

∴∠ACD=∠CDE，

∴GE∥AC，

∴四边形ACEG是平行四边形，

∴AG∥CE，

又∵矩形CEFG中，GF∥CE，

∴AG和GF在同一条直线上．（过直线外一点有且只有一条直线与已知直线平行）