题目内容
①(-10)2+(-10)0+(
)-1;
②(x-
)2.
③已知m=2,n=1,求[(3mn+1)(3mn-1)+3mn+1]÷m的值.
④已知a+b=10,ab=24,求(a-b)2.
| 1 |
| 2 |
②(x-
| 1 |
| 2 |
③已知m=2,n=1,求[(3mn+1)(3mn-1)+3mn+1]÷m的值.
④已知a+b=10,ab=24,求(a-b)2.
分析:①原式第一项表示两个-10的乘积,第二项利用零指数公式化简,最后一项利用负指数公式化简,计算即可得到结果;
②原式利用完全平方公式展开即可;
③原式中括号中第一项利用平方差公式化简,合并后利用多项式除以单项式法则计算,得到最简结果,将m与n的值代入计算,即可求出值;
④原式利用完全平方公式展开,配方后将a+b及ab的值代入计算,即可求出值.
②原式利用完全平方公式展开即可;
③原式中括号中第一项利用平方差公式化简,合并后利用多项式除以单项式法则计算,得到最简结果,将m与n的值代入计算,即可求出值;
④原式利用完全平方公式展开,配方后将a+b及ab的值代入计算,即可求出值.
解答:解:①原式=100+1+2
=103;
②原式=x2-x+
;
③原式=(9m2n2-1+3mn+1)÷m
=(9m2n2+3mn)÷m
=9mn2+3n,
当m=2,n=1时,原式=9×2×1+3=21;
④∵a+b=10,ab=24,
∴原式=a2-2ab+b2=(a+b)2-4ab
=100-96
=4.
=103;
②原式=x2-x+
| 1 |
| 4 |
③原式=(9m2n2-1+3mn+1)÷m
=(9m2n2+3mn)÷m
=9mn2+3n,
当m=2,n=1时,原式=9×2×1+3=21;
④∵a+b=10,ab=24,
∴原式=a2-2ab+b2=(a+b)2-4ab
=100-96
=4.
点评:此题考查了整式的混合运算-化简求值,以及实数的混合运算,涉及的知识有:完全平方公式,平方差公式,单项式乘以多项式法则,去括号法则,以及合并同类项法则,熟练掌握公式及法则是解本题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
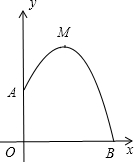 图)如果抛物线的最高点M离墙1米,离地面
图)如果抛物线的最高点M离墙1米,离地面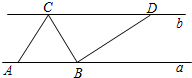 12、如图,直线a∥b,点A、B位于直线a上,点C、D位于直线b上,且AB:CD=1:2,若△ABC的面积为5,则△BCD的面积为
12、如图,直线a∥b,点A、B位于直线a上,点C、D位于直线b上,且AB:CD=1:2,若△ABC的面积为5,则△BCD的面积为