题目内容
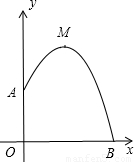
某幢建筑物，从10米高的窗口A用水管和向外喷水，喷的水流呈抛物线（抛物线所在平面与墙面垂直），（如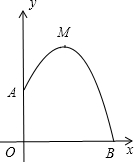
图）如果抛物线的最高点M离墙1米，离地面
米，则水流下落点B离墙距离OB是（ ）
图）如果抛物线的最高点M离墙1米，离地面| 40 |
| 3 |
| A、2米 | B、3米 | C、4米 | D、5米 |
分析：以地面，墙面所在直线为x轴，y轴建立平面直角坐标系，把题中已知点代入，求出解析式后，令y=0，即可解答．
解答：解：设抛物线解析式：y=a（x-1）2+
，
把点A（0，10）代入抛物线解析式得：
a=-
，
∴抛物线解析式：
y=-
（x-1）2+
．
当y=0时，x1=-1（舍去），x2=3．
∴OB=3米．
故选B．
| 40 |
| 3 |
把点A（0，10）代入抛物线解析式得：
a=-
| 10 |
| 3 |
∴抛物线解析式：
y=-
| 10 |
| 3 |
| 40 |
| 3 |
当y=0时，x1=-1（舍去），x2=3．
∴OB=3米．
故选B．
点评：本题考查抛物线建模，在平面直角坐标系中求抛物线解析式，解决实际问题．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
某幢建筑物，从10米高的窗口A用水管和向外喷水，喷的水流呈抛物线，抛物线所在平面与墙面垂直（如图），如果抛物线的最高点M离墙1米，离地面
某幢建筑物，从10米高的窗口A用水管向外喷水，喷出的水流呈抛物线状（抛物线所在平面与墙面垂直，如图），如果抛物线的最高点M离墙1米，离地面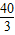
米，则水流下落点B离墙距离OB是（ ）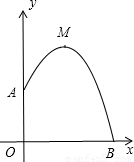
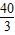米，则水流下落点B离墙距离OB是（ ）