题目内容
【题目】小李在学校“青少年科技创新比赛”活动中，设计了一个沿直线轨道做匀速直线运动的模型．甲车从
处出发向
处行驶，同时乙车从处出发向处行驶．如图所示，线段
、
分别表示甲车、乙车离处的距离
（米）与已用时间
（分）之间的关系．试根据图象，解决以下问题：
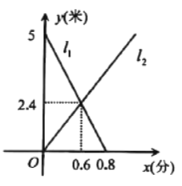
（1）填空：出发_________（分）后，甲车与乙车相遇，此时两车距离处________（米）；
（2）求乙车行驶
（分）时与处的距离．
【答案】（1）0.6，2.4；（2）4.8米
【解析】
（1）甲乙相遇即图象交点（0.6，2.4）
（2）根据图象解出两条直线的解析式，再由题意得到乙车行驶1.2（分）时与B处的距离．
（1）甲乙相遇即图象交点（0.6，2.4）
∴出发0.6（分）后，甲车与乙车相遇，此时两车距离B处2.4（米）；
故答案为0.6和2.4
（2）假设直线l2的解析式为y=kx，将点（0.6，2.4）代入得，y=4x
当x=1.2时，y=4.8
∴乙车行驶12（分）时与B处距离为4.8米．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某校为灾区开展了"献出我们的爱"赈灾捐款活动，九年级（1）班50名同学积极参加了这次赈灾捐款活动，
捐款（元） | 10 | 15 | 30 |
| 50 | 60 |
人数 | 3 | 6 | 11 |
| 13 | 6 |
因不慎，表中数据有两处被墨水污染，已无法看清，但已知全班平均每人捐款38元
（1）根据以上信息请帮助小明计算出被污染处的数据，并写出解答过程．
（2）该班捐款金额的众数，中位数分别是多少？
（3）如果用九年级（1）班捐款情况作为一个样本，请估计全校1200人中捐款在40元以上（包括40元）的人数是多少？
