题目内容
如图，已知△ABC三边长相等，和点P，设点P到△ABC三边AB、AC、BC（或其延长线）的距离分别为
h1、h2、h3，△ABC的高为h．在图（1）中， 点P是边BC的中点，由S△ABP+S△ACP=S△ABC得
，可得
又因为h3=0，所以：
．
图（2）~（5）中，点P分别在线段MC上、MC延长线上、△ABC内、△ABC外．
h1、h2、h3，△ABC的高为h．在图（1）中， 点P是边BC的中点，由S△ABP+S△ACP=S△ABC得
，可得又因为h3=0，所以：．图（2）~（5）中，点P分别在线段MC上、MC延长线上、△ABC内、△ABC外．
（1）请探究：图（2）~（5）中， h1、h2、h3、h之间的关系；（直接写出结论）
（2）说明图（2）所得结论为什么是正确的；
（3）说明图（5）所得结论为什么是正确的．
（2）说明图（2）所得结论为什么是正确的；
（3）说明图（5）所得结论为什么是正确的．
（1）图②-⑤ 中的关系依次是： h1+h2+h3=h； h1-h2+h3=h； h1+h2+h3=h； h1+h2-h3=h；
（2）图②中，h1+h2+h3=h．连结AP，
则SΔAPB+SΔAPC=SΔABC．
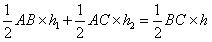
又 h3=0，AB=AC=BC， ∴ h1+h2+h3==h；
（3）：图⑤中，h1+h2-h3=h．连接PA、PB、PC，则SΔAPB+SΔAPC=SΔABC+SΔBPC．
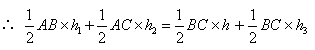
又 AB=AC=BC， ∴h1+h2 =h+h3．
∴ h1+h2-h3=h
（2）图②中，h1+h2+h3=h．连结AP，
则SΔAPB+SΔAPC=SΔABC．
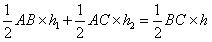
又 h3=0，AB=AC=BC， ∴ h1+h2+h3==h；
（3）：图⑤中，h1+h2-h3=h．连接PA、PB、PC，则SΔAPB+SΔAPC=SΔABC+SΔBPC．
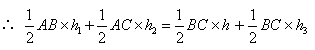
又 AB=AC=BC， ∴h1+h2 =h+h3．
∴ h1+h2-h3=h
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
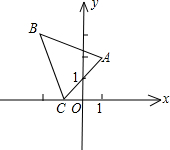如图，已知△ABC三个顶点的坐标分别为（1，2），（-2，3），（-1，0），把它们的横坐标和纵坐标都扩大到原来的2倍，得到点A′，B′，C′．下列说法正确的是（ ）| A、△A′B′C′与△ABC是位似图形，位似中心是点（1，0） | B、△A′B′C′与△ABC是位似图形，位似中心是点（0，0） | C、△A′B′C′与△ABC是相似图形，但不是位似图形 | D、△A′B′C′与△ABC不是相似图形 |
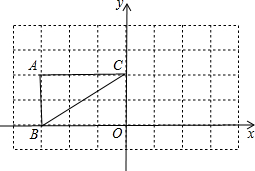如图，已知△ABC三个顶点的坐标分别为：A（-3，2）、B（-3，0）、C（0，2），
如图，已知△ABC三个顶点的坐标分别为A（-2，3），B（-6，0），C（-1，0）．
如图，已知△ABC三个顶点的坐标分别为A（-2，3），B（-6，0），C（-1，0）
在平面直角坐标系中，如图，已知△ABC三个顶点的坐标分别为A（1，-4），B（5，-4），C（4，-1），