题目内容

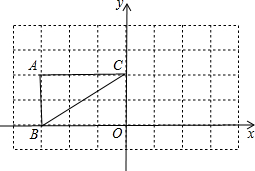精英家教网如图，已知△ABC三个顶点的坐标分别为：A（-3，2）、B（-3，0）、C（0，2），
①写出A、B、C关于y轴对称的对称点A′、B′、C′的坐标；
②作出△A′B′C′；
③求△BCB′的面积．
分析：①关于y轴对称的点，横坐标互为相反数，纵坐标相等，依此写出点A′、B′、C′的坐标；
②连接A′B′，B′C′，A′C′即可；
③观察图形，直接求出BB′，CO的长，再求面积．
解答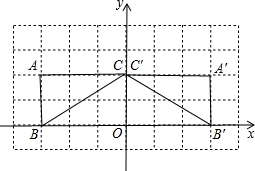：精英家教网解：①∵关于y轴对称的点，横坐标互为相反数，纵坐标相等，
∴A′（3，2）、B′（3，0）、C′（0，2）；
②作出△A′B′C′如图，

③由图形可知：BB′=6，CO=2，BB′⊥CO
∴S△BCB’=
1
2
×BB′×CO=
1
2
×6×2=6．
点评：本题考查了关于y轴对称的点的坐标特点，图形的画法及利用坐标求面积的问题．
练习册系列答案
相关题目
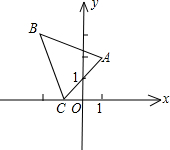精英家教网如图，已知△ABC三个顶点的坐标分别为（1，2），（-2，3），（-1，0），把它们的横坐标和纵坐标都扩大到原来的2倍，得到点A′，B′，C′．下列说法正确的是（　　）
A、△A′B′C′与△ABC是位似图形，位似中心是点（1，0）B、△A′B′C′与△ABC是位似图形，位似中心是点（0，0）C、△A′B′C′与△ABC是相似图形，但不是位似图形D、△A′B′C′与△ABC不是相似图形
如图，已知△ABC三个顶点的坐标分别为A（-2，3），B（-6，0），C（-1，0）．
（1）直接写出A点关于y轴对称的点的坐标是
（2，3）
（2，3）
；
（2）将△ABC向右平移三个单位后，再关于y轴对称得△A′B′C′，画出图形，且A′的坐标为
（1，-3）
（1，-3）
；
（3）若△DBC与△ABC全等，D不与A重合，则D点的坐标为
（-2，-3）或（-5，-3）或（-5，3）
（-2，-3）或（-5，-3）或（-5，3）
．
如图，已知△ABC三个顶点的坐标分别为A（-2，3），B（-6，0），C（-1，0）
（1）直接写出A点关于y轴对称的点的坐标是
（2，3）
（2，3）
；
（2）将△ABC向右平移三个单位后，再关于x轴对称得△A′B′C′，画出图形，且A′的坐标为
（1，-3）
（1，-3）
；
（3）若△DBC与△ABC全等，D不与A重合，则D点的坐标为
（-5，3），（-2，-3），（-5，-3）
（-5，3），（-2，-3），（-5，-3）
．
在平面直角坐标系中，如图，已知△ABC三个顶点的坐标分别为A（1，-4），B（5，-4），C（4，-1），
（1）画出△ABC；
（2）将△ABC先向上平移2个单位长度，再向左平移4个单位长度后得到△A′B′C′，画出△A′B′C′．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网