Question

【题目】已知：，OB，OM，ON是内的射线．

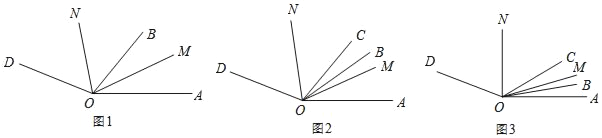
如图1，若OM平分，ON平分当射线OB绕点O在内旋转时，______度

也是内的射线，如图2，若，OM平分，ON平分，当绕点O在内旋转时，求的大小．

在的条件下，若，当在绕O点以每秒的速度逆时针旋转t秒，如图3，若：：3，求t的值．

Answer 1

【答案】(1) 80；(2) 70°；（3）t为21秒．

【解析】

（1）因为∠AOD=160°，OB、OC、OM、ON是∠AOD内的射线．若OM平分∠AOB，ON平分∠BOD，则 然后根据关系转化求出角的度数；
（2）利用各角的关系求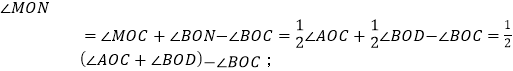

（3）由题意得

由此列出方程求解即可．

解：（1）∵OM平分∠AOB，ON平分∠BOD，

∴

∴∠MON=∠BOM+∠BON

=80°，

故答案为：80；

（2）∵OM平分∠AOC，ON平分∠BOD，

∴

即∠MON=∠MOC+∠BON﹣∠BOC

=70°；

又∵∠AOM：∠DON=2：3，

∴3（30°+2t）=2（150°﹣2t），

得t=21．

答：t为21秒．