题目内容
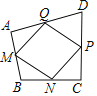
【题目】如图,已知:点A、B、C、D在⊙O上,AB=CD,下列结论:①∠AOC=∠BOD;②∠BOD=2∠BAD;③AC=BD;④∠CAB=∠BDC;⑤∠CAO+∠CDO=180°.其中正确的个数为( )
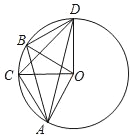
A. 2 B. 3 C. 4 D. 5
【答案】C
【解析】
根据圆内接四边形的性质、圆周角定理和圆心角、弧、弦之间的关系逐个判断即可.
∵AB=CD,
∴![]() ,
,
∴![]() ,
,
∴∠AOC=∠BOD,故①正确;
∵圆周角∠BAD和圆心角∠BOD都对着![]() ,
,
∴∠BOD=2∠BAD,故②正确;
∵![]() ,
,
∴AC=BD,故③正确;
∵圆周角∠CAB和∠BDC都对着![]() ,
,
∴∠CAB=∠BDC,故④正确;
延长DO交⊙O于M,连接AM,
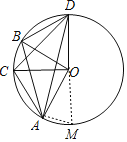
∵D、C、A、M四点共圆,
∴∠CDO+∠CAM=180°(圆内接四边形对角互补),
∵∠CAM>∠CAO,
∴∠CAO+∠CDO<180°,故⑤错误;
即正确的个数是4个,
故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
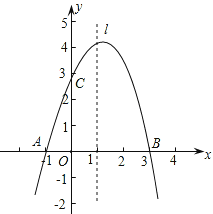
【题目】某超市准备购进甲、乙两种品牌的文具盒,甲、乙两种玩具盒的进价和售价如下表,预计购进乙品牌文具盒的数量y(个)与甲品牌玩具盒数量x(个)之间的函数关系如图所示.
甲 | 乙 | |
进价(元) | 15 | 30 |
售价(元) | 20 | 38 |
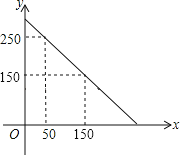
(1)y与x之间的函数关系式是 ;
(2)若超市准备用不超过6000元购进甲、乙两种文具盒,则至少购进多少个甲种文具盒?
(3)在(2)的条件下,写出销售所得的利润W(元)与x(个)之间的关系式,并求出获得的最大利润.