题目内容
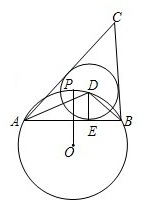 如图,⊙O的半径为1,点P是⊙O上一点,弦AB垂直平分线段OP.点D是弦AB所对劣弧上的任一点(异于点A、B),过点D作DE⊥AB于点E,以点D为圆心,DE长为半径作⊙D,连接AD、BD.分别过点A、B作⊙D的切线,两条切线交于点C.下列结论:
如图,⊙O的半径为1,点P是⊙O上一点,弦AB垂直平分线段OP.点D是弦AB所对劣弧上的任一点(异于点A、B),过点D作DE⊥AB于点E,以点D为圆心,DE长为半径作⊙D,连接AD、BD.分别过点A、B作⊙D的切线,两条切线交于点C.下列结论:
①AB= ;②∠ACB为定值60°;③∠ADB=2∠ACB;④设△ABC的面积为S,若
;②∠ACB为定值60°;③∠ADB=2∠ACB;④设△ABC的面积为S,若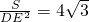 则△ABC的周长为3.
则△ABC的周长为3.
其中正确的有
- A.①②③
- B.①②④
- C.②③④
- D.①③④
A
分析:①在RT△AOF中求出AF,然后可得出AB的长度;②求出AOB,然后利用圆周角的知识求出∠ADB,继而可得出∠C;③根据②的解答过程即可判断出正确与否;④根据切线的性质表示出△ABC的面积,然后根据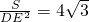 ,解出DE,继而可得出周长.
,解出DE,继而可得出周长.
解答:①
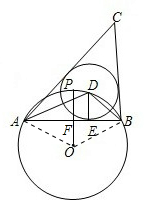
由题意得,OF= 、OA=1,在RT△AOF中,可得AF=
、OA=1,在RT△AOF中,可得AF= ,从而可得AB=2AF=
,从而可得AB=2AF= ,故①正确;
,故①正确;
②由OF= OA,可得∠AOF=60°,从而∠AOB=120°,即劣弧AB=120°,优弧AB=240°,从而∠ADB=120°,
OA,可得∠AOF=60°,从而∠AOB=120°,即劣弧AB=120°,优弧AB=240°,从而∠ADB=120°,
∵∠C+∠CAB+∠CBA=180°,∠ADB+ (∠CAB+∠CBA)=180°,
(∠CAB+∠CBA)=180°,
∴解得∠C=60°,故②正确;
③根据②的证明过程可得出∠ADB=120°,∠C=60°,故可得∠ADB=2∠ACB,即③正确;
④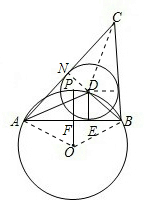
由①得,AB= ,
,
∵△ABC的面积为S= (AB+AN+CN+BC)×DE=
(AB+AN+CN+BC)×DE= (2
(2 +2CN)×DE,
+2CN)×DE,
∵△ABC的面积为S,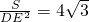 ,
,
∴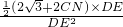 =4
=4 ,
,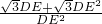 ,
,
∵DE=DN= CD,
CD,
∴CN= DE,
DE,
∴可得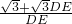 =4
=4 ,
,
解得:DE= ,
,
△ABC的周长=AB+AC+BC=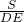 =4
=4 DE=
DE= 故④错误.
故④错误.
综上可得①②③正确.
故选A.
点评:此题考属于圆的综合题目,涉及了切线的性质、角平分线的性质、三角形的面积,④的判断比较麻烦,需要先求出DE的长度,对于此类题目可以利用排除法来作,这样可以省下不少时间.
分析:①在RT△AOF中求出AF,然后可得出AB的长度;②求出AOB,然后利用圆周角的知识求出∠ADB,继而可得出∠C;③根据②的解答过程即可判断出正确与否;④根据切线的性质表示出△ABC的面积,然后根据
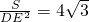 ,解出DE,继而可得出周长.
,解出DE,继而可得出周长.解答:①

由题意得,OF=
 、OA=1,在RT△AOF中,可得AF=
、OA=1,在RT△AOF中,可得AF= ,从而可得AB=2AF=
,从而可得AB=2AF= ,故①正确;
,故①正确;②由OF=
 OA,可得∠AOF=60°,从而∠AOB=120°,即劣弧AB=120°,优弧AB=240°,从而∠ADB=120°,
OA,可得∠AOF=60°,从而∠AOB=120°,即劣弧AB=120°,优弧AB=240°,从而∠ADB=120°,∵∠C+∠CAB+∠CBA=180°,∠ADB+
 (∠CAB+∠CBA)=180°,
(∠CAB+∠CBA)=180°,∴解得∠C=60°,故②正确;
③根据②的证明过程可得出∠ADB=120°,∠C=60°,故可得∠ADB=2∠ACB,即③正确;
④

由①得,AB=
 ,
,∵△ABC的面积为S=
 (AB+AN+CN+BC)×DE=
(AB+AN+CN+BC)×DE= (2
(2 +2CN)×DE,
+2CN)×DE,∵△ABC的面积为S,
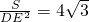 ,
,∴
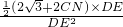 =4
=4 ,
,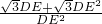 ,
,∵DE=DN=
 CD,
CD,∴CN=
 DE,
DE,∴可得
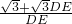 =4
=4 ,
,解得:DE=
 ,
,△ABC的周长=AB+AC+BC=
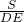 =4
=4 DE=
DE= 故④错误.
故④错误.综上可得①②③正确.
故选A.
点评:此题考属于圆的综合题目,涉及了切线的性质、角平分线的性质、三角形的面积,④的判断比较麻烦,需要先求出DE的长度,对于此类题目可以利用排除法来作,这样可以省下不少时间.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 如图,⊙O的半径为5,AB=5
如图,⊙O的半径为5,AB=5 如图,⊙O的半径为3,直径AB⊥弦CD,垂足为E,点F是BC的中点,那么EF2+OF2=
如图,⊙O的半径为3,直径AB⊥弦CD,垂足为E,点F是BC的中点,那么EF2+OF2= 如图,⊙O的半径为
如图,⊙O的半径为 如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离.
如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离. 如图,⊙O的半径为5,P是弦MN上的一点,且MP:PN=1:2.若PA=2,则MN的长为
如图,⊙O的半径为5,P是弦MN上的一点,且MP:PN=1:2.若PA=2,则MN的长为