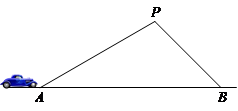题目内容
如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=5,E为DC中点,tan∠C=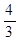 .则AE的长度为_ __.
.则AE的长度为_ __.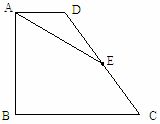
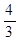 .则AE的长度为_ __.
.则AE的长度为_ __.
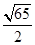
试题分析:先过E作BC的垂线,交BC于F,交AD延长线于M,根据AAS证明△MDE≌△FCE,得出EF=ME,DM=CF,可求得DM的长,再通过解直角三角形可求得MF的长,最后利用勾股定理求得AE的长.
过点E作BC的垂线交BC于点F,交AD的延长线于点M,
∵AD∥BC,E是DC的中点,
∴∠M=∠MFC,DE=CE;
在△MDE和△FCE中,
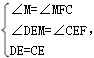
∴△MDE≌△FCE,
∴EF=ME,DM=CF.
∵AD=2,BC=5,
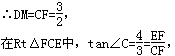
∴EF=ME=2,
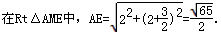
点评:此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
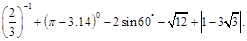
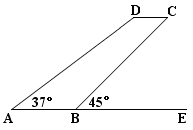
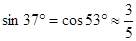 ,
,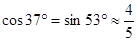 ,
,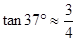 )
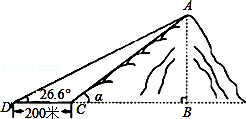
)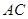 的坡度是
的坡度是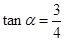 ,在与山脚
,在与山脚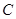 距离
距离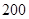 米的
米的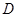 处,测得山顶
处,测得山顶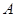 的仰角为
的仰角为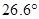 ,求小山岗的高
,求小山岗的高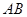 (结果取整数:参考数据:
(结果取整数:参考数据: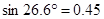 ,
,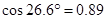 ,
,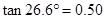 ).
).
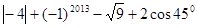
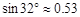 ,
,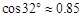 ,
,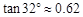 ,
,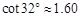 )
)