题目内容
【题目】如图,抛物线过x轴上两点A(9,0),C(-3,0),且与y轴交于点B(0,-12).
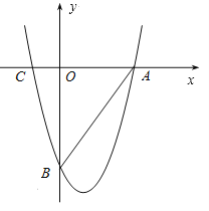
(1)求抛物线的解析式;
(2)若动点P从点A出发,以每秒2个单位沿射线AC方向运动;同时,点Q从点B出发,以每秒1个单位沿射线BA方向运动,当点P到达点C处时,两点同时停止运动.问当t为何值时,△APQ∽△AOB?
(3)若M为线段AB上一个动点,过点M作MN平行于y轴交抛物线于点N.
①是否存在这样的点M,使得四边形OMNB恰为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
②当点M运动到何处时,四边形CBNA的面积最大?求出此时点M的坐标及四边形CBNA面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①不存在;②当点M运动到(
;(3)①不存在;②当点M运动到(![]() ,-6)时,四边形CBNA的面积最大,四边形CBNA面积的最大值为
,-6)时,四边形CBNA的面积最大,四边形CBNA面积的最大值为![]() .
.
【解析】
试题(1)应用待定系数法,设交点式求解;
(2)根据相似三角形的性质求解即可;
(3)①由MN=OB=12列式,根据一元二次方程根的判别式小于0得出不存在这样的点M,使得四边形OMNB恰为平行四边形结论;②求出面积关于x的二次函数关系式,应用二次函数最值原理求解即可.
试题解析:(1)因抛物线过x轴上两点A(9,0),C(-3,0),故设抛物线解析式为:![]() .
.
又∵B(0,-12) ∴![]() ,解得a=
,解得a=![]() 。
。
∴抛物线的解析式为![]() .
.
(2)∵OA=9,OB=12,∴AB=15.
∵点P的速度是每秒2个单位,点Q的速度是每秒1个单位,∴AP=2t,AQ=15-t.
又∵AC=12,∴0≤t≤6.
∵△APQ∽△AOB,∴![]() ,即
,即![]() ,解得
,解得![]() .
.
∴当![]() 时,△APQ∽△AOB.
时,△APQ∽△AOB.
(3)易求直线AB的函数关系式为![]() .
.
设点M的横坐标为x,则M(x,![]() ),N(x,
),N(x,![]() ).
).
①若四边形OMNB为平行四边形,则MN=OB=12
∴![]() ,即x2-9x+27=0.
,即x2-9x+27=0.
∵△<0,∴此方程无实数根.
∴不存在这样的点M,使得四边形OMNB恰为平行四边形.
②∵S四边形CBNA=S△ACB+S△ABN="72+" S△ABN
∵S△AOB=54,S△OBN=6x,S△OAN=![]() ·9·
·9·![]() =-2x2+12x+54
=-2x2+12x+54
∴S△ABN=S△OBN+S△OAN-S△AOB=6x+(-2x2+12x+54)-54=-2x2+18x=![]() .
.
∴当x=![]() 时,S△ABN最大值=
时,S△ABN最大值=![]() ,此时M(
,此时M(![]() ,-6)
,-6)
S四边形CBNA最大=![]() .
.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案【题目】在水果销售旺季,某水果店购进一优质水果,进价为 20 元/千克,售价不低于 20 元/千克,且不超过 32 元/千克,根据销售情况,发现该水果一天的销售量 y(千克)与该天的售价 x(元/千克)满足如下表所示的一次函数关系.
销售量 y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价 x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为 23.5 元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利 150 元,那么该天水果的售价为多少元?