题目内容
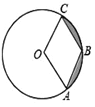
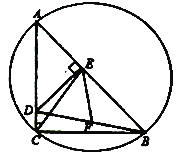
【题目】如图,![]() 是
是![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ;点
;点![]() 是
是![]() 延长线上一点,
延长线上一点,![]() ,
,![]() .
.
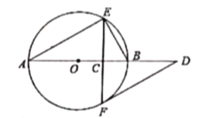
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,若
,若![]() 的半径为2,求
的半径为2,求![]() 的长.
的长.
【答案】(1)见解析(2)![]()
【解析】
(1)连接OE,OF,由垂径定理和圆周角定理得到∠DOF=∠DOE.而∠DOE=2∠A,得出∠DOF=2∠A,证出∠OFD=90°.即可得出结论;
(2)连接OM,由垂径定理和勾股定理进行计算即可.
(1)连接OE,OF,如图1所示:
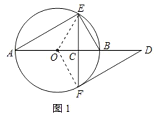
∵EF⊥AB,AB是⊙O的直径,
∴![]() ,
,
∴∠DOF=∠DOE,
∵∠DOE=2∠A,∠A=30°,
∴∠DOF=60°,
∵∠D=30°,
∴∠OFD=90°.
∴OF⊥FD.
∴FD为⊙O的切线;
(2)连接OM.如图2所示:

∵O是AB中点,M是BE中点,
∴OM∥AE.
∴∠MOB=∠A=30°.
∵OM过圆心,M是BE中点,
∴OM⊥BE.
∴MB=![]() OB=1,OM=
OB=1,OM=![]() =
=![]() .
.
∵∠DOF=60°,
∴∠MOF=90°.
∴MF=![]() .
.

练习册系列答案
相关题目