Question

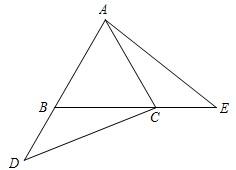23、已知：如图，在等边三角形ABC中，点D、E分别在边AB、BC的延长线上，且AD=BE，连接AE、CD．
（1）求证：△CBD≌△ACE；
（2）如果AB=3cm，那么△CBD经过怎样的图形运动后，能与△ACE重合？请写出你的具体方案．（可以选择的图形运动是指：平移、旋转、翻折）

Answer 1

分析：（1）围绕“SAS”的判定方法，找证明△CBD≌△ACE的条件；
（2）围绕平移、旋转、翻折，或者两种变换的组合，寻找变换的不同方法．

解答：（1）证明：在等边三角形ABC中，
∵AD=BE，AB=BC，
∴BD=CE，（2分）
又∵∠ABC=∠ACB=60°，
∴∠CBD=∠ACE，（2分）
∵CB=AC，
∴△ACE≌△CBD．（2分）

（2）解：
方法一：绕正三角形的中心逆时针旋转120°．（6分）
（注：如果运用此种方法，那么讲清旋转中心“正三角形的中心”，得（3分）；讲清“逆时针旋转120°”，得3分）
方法二：绕点C逆时针旋转120°，再沿CA方向平移3cm．（6分）
方法三：绕点B逆时针旋转120°，再沿BC方向平移3cm．（6分）
方法四：绕点A逆时针旋转60°，再绕点C逆时针旋转60°．（6分）
（注：不管经过几次运动，只要正确都可得分、如果分两次运动得到，那么讲清每一种运动均可得（3分）：如果讲出旋转，那么得（1分），如果讲清方向和旋转角的大小，那么得（2分）；如果讲出平移，那么得（1分），如果讲清平移的方向和距离，那么得2分）

点评：本题考查了运用旋转的性质证明三角形全等的方法，综合运用平移、旋转、翻折和设计图形变换的能力．