题目内容
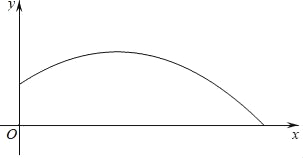
【题目】抛物线y＝ax2＋bx＋c上部分点的横坐标x，纵坐标y的对应值如下表所示.
x | … | －3 | －2 | －1 | 0 | 1 | … |
y | … | －12 | －2 | 4 | 6 | 4 | … |
给出下列说法：①抛物线与y轴的交点为(0，6)；②抛物线的对称轴是在y轴的右侧；③抛物线一定经过点(3，0)；④当x<0时，函数值y随x的增大而减小．
从表中可知，上述说法正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】A
【解析】
根据表中的数据与抛物线的对称性，可得抛物线的开口向下，对称轴为x=0，由此可作出判断.
根据表格，抛物线与y轴交于（0,6），①正确；
∵抛物线经过点（-1,4）和（1,4），
∴对称轴为x=
=0，故②错误；
∵抛物线经过（-3.-12），根据对称性也会经过（3，-12），故③错误；
由对称轴为x=0，知当x<0时，函数值y随x的增大而增大，故④错误；
所以正确个数为1，选A.
练习册系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
