题目内容
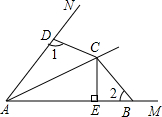
如图,已知点C是∠MAN的平分线上一点,CE⊥AB于E,B、D分别在AM、AN上,且AE=
(AD+AB).问:∠1和∠2有何关系?
| 1 |
| 2 |

略证:∠1与∠2互补.
法1:作CF⊥AN于F(如图),
∵∠3=∠4,CE⊥AM,
∴CF=CE,∠CFA=∠CEA=90°,
在Rt△ACF≌Rt△ACE(HL),
∴AF=AE.
∵AE=
(AD+AB)=
(AF-DF+AE+EB)=AE+
(BE-DF),
∴BE-DF=0,
∴BE=DF,
∴△DFC≌△BEC(SAS),
∴∠5=∠2,
∵∠1+∠5=180°,
∴∠1+∠2=180°;
法2:在AM上截取AF=AD,连接CF(如图),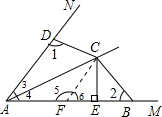
∵∠3=∠4,AC为公共边,
∴△ADC≌△AFC,
∴∠1=∠5,
∵AE=
(AD+AB)=
(AF+AE+EB)=
(AE-EF+AE+EB),
∴EB-EF=0,所以EF=EB,
又∵CE⊥AB,
∴BC=FC,∴∠2=∠6,
∵∠5+∠6=180°,
∴∠1+∠2=180°.
法1:作CF⊥AN于F(如图),
∵∠3=∠4,CE⊥AM,
∴CF=CE,∠CFA=∠CEA=90°,
在Rt△ACF≌Rt△ACE(HL),
∴AF=AE.
∵AE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴BE-DF=0,
∴BE=DF,
∴△DFC≌△BEC(SAS),
∴∠5=∠2,
∵∠1+∠5=180°,
∴∠1+∠2=180°;
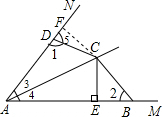
法2:在AM上截取AF=AD,连接CF(如图),

∵∠3=∠4,AC为公共边,
∴△ADC≌△AFC,
∴∠1=∠5,
∵AE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴EB-EF=0,所以EF=EB,
又∵CE⊥AB,
∴BC=FC,∴∠2=∠6,
∵∠5+∠6=180°,
∴∠1+∠2=180°.


练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目