题目内容
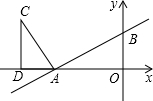 如图,在直角坐标系中,直线
如图,在直角坐标系中,直线 与x轴、y轴分别交于A、B两点,过点A作CA⊥AB,CA=
与x轴、y轴分别交于A、B两点,过点A作CA⊥AB,CA= ,并且作CD⊥x轴.
,并且作CD⊥x轴.
(1)求证:△ADC∽△BOA;
(2)若抛物线y=-x2+bx+c经过B、C两点.
①求抛物线的解析式;
②该抛物线的顶点为P,M是坐标轴上的一个点,若直线PM与y轴的夹角为30°,请直接写出点M的坐标.
解:(1)∵CD⊥AB
∴∠BAC=90°
∴∠BAO+∠CAD=90°
∵CD⊥x轴
∴∠CDA=90°
∴∠C+∠CAD=90°
∴∠C=∠BAO
又∵∠CDO=∠AOB=90°
∴△ADC∽△BOA;
(2)①由题意得,A(-8,0),B(0,4)
∴OA=8,OB=4,AB=
∵△ADC∽△BOA,CA=
∴AD=2,CD=4
∴C(-10,4)
将B(0,4),C(-10,4)代入y=-x2+bx+c
∴ .
.
∴y=-x2-10x+4
②M1(0,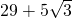 ),M2(0,
),M2(0,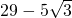 ),M3(
),M3( ,0),M4(
,0),M4(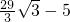 ,0).
,0).
分析:(1)根据互余关系易得∠C=∠BAO,又有∠CDO=∠AOB=90°,易得△ADC∽△BOA;
(2)①由题意得,A、B的坐标,结合(1)的结论,得到AD、CD的长,进而可得抛物线的解析式;
②根据P的坐标及三角函数的意义,易得点M的坐标.
点评:本题考查学生将二次函数的图象与解析式相结合处理问题、解决问题的能力.
∴∠BAC=90°
∴∠BAO+∠CAD=90°
∵CD⊥x轴
∴∠CDA=90°
∴∠C+∠CAD=90°
∴∠C=∠BAO
又∵∠CDO=∠AOB=90°
∴△ADC∽△BOA;
(2)①由题意得,A(-8,0),B(0,4)
∴OA=8,OB=4,AB=

∵△ADC∽△BOA,CA=

∴AD=2,CD=4
∴C(-10,4)
将B(0,4),C(-10,4)代入y=-x2+bx+c

∴
 .
.∴y=-x2-10x+4
②M1(0,
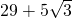 ),M2(0,
),M2(0,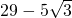 ),M3(
),M3( ,0),M4(
,0),M4(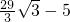 ,0).
,0).分析:(1)根据互余关系易得∠C=∠BAO,又有∠CDO=∠AOB=90°,易得△ADC∽△BOA;
(2)①由题意得,A、B的坐标,结合(1)的结论,得到AD、CD的长,进而可得抛物线的解析式;
②根据P的坐标及三角函数的意义,易得点M的坐标.
点评:本题考查学生将二次函数的图象与解析式相结合处理问题、解决问题的能力.

练习册系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: