题目内容
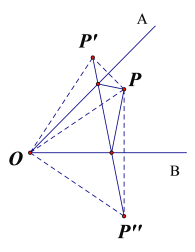
【题目】已知∠AOB=45°,点P在∠AOB的内部.P′与P关于OA对称,P"与P关于OB对称,则O、P′、P"三点所构成的三角形是( )

A.直角三角形B.钝角三角形C.等腰直角三角形D.等边三角形
【答案】C
【解析】
本题关键是根据轴对称,得到相等的角,进行相加得到直角,再得到三条线段P'O=PO= P'O,从而得到是等腰直角三角形.
解:如下图所示,连结P'O、PO、P'O,
∵P'与P关于OA对称
∴∠P'OA=∠POA ,P'O=PO
同理∠P'OB=∠POB ,P'O=PO
∠POA+∠POB=∠AOB=45°
∴∠P'OA+∠P'OB=∠POA+∠POB=45°
∴∠P'OA+∠P'OB+∠POA+∠POB=45°+45°=90°
∴△OP 'P'是直角三角形.
由P'O=PO和 P'O=PO得P'O= P'O
∴△OP'P'是等腰直角三角形.
故选C.

练习册系列答案
相关题目