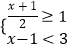Question

【题目】对于数轴上的点P，Q，给出如下定义：若点P到点Q的距离为d(d≥0)，则称d为点P到点Q的d追随值，记作d[PQ]．例如，在数轴上点P表示的数是2，点Q表示的数是5，则点P到点Q的d追随值为d[PQ]=3．

问题解决：

(1)点M，N都在数轴上，点M表示的数是1，且点N到点M的d追随值d[MN]=a(a≥0)，则点N表示的数是_____(用含a的代数式表示)；

(2)如图，点C表示的数是1，在数轴上有两个动点A，B都沿着正方向同时移动，其中A点的速度为每秒3个单位，B点的速度为每秒1个单位，点A从点C出发，点B表示的数是b，设运动时间为t(t>0)．

①当b=4时，问t为何值时，点A到点B的d追随值d[AB]=2；

②若0<t≤3时，点A到点B的d追随值d[AB]≤6，求b的取值范围．

Answer 1

【答案】(1)1＋a或1－a；(2)或；(3)1≤b≤7.

【解析】

(1)根据d追随值的定义，分点N在点M左侧和点N在点M右侧两种情况，直接写出答案即可；

(2)①分点A在点B左侧和点A在点B右侧两种情况，类比行程问题中的追及问题，根据“追及时间=追及路程÷速度差”计算即可；②

解：(1)点N在点M右侧时，点N表示的数是1+a；

点N在点M左侧时，点N表示的数是1-a；

(2)①b=4时，AB相距3个单位，

当点A在点B左侧时，t=(3-2)÷(3-1)=，

当点A在点B右侧时，t=(3+2)÷(3-1)=；

②当点B在点A左侧或重合时，即d≤1时，随着时间的增大，d追随值会越来越大，

∵0<t≤3，点A到点B的d追随值d[AB]≤6，

∴1-d+3×(3-1)≤6，

解得d≥1，

∴d=1，

当点B在点A右侧时，即d>1时，在AB重合之前，随着时间的增大，d追随值会越来越小，

∵点A到点B的d追随值d[AB]≤6，∴d≤7

∴1<d≤7，

综合两种情况，d的取值范围是1≤d≤7.

故答案为：(1)1＋a或1－a；(2)①或；②1≤b≤7.