题目内容
如图,AB是半圆O的直径,CD垂直AB于D,EC是切线,E为切点.求证:CE=CF。
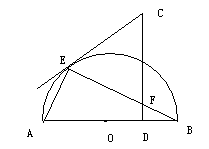

连接EO,
∵EC是切线,E为切点,
∴EO⊥EC,
∴∠1+∠2=90°,
∵AB是半圆O的直径,CD垂直AB于D,
∴∠FDB=90°,
∴∠FBD+∠4=90°,
∵∠1=∠FBD,∠3=∠4,
∴∠4=∠3=∠2,
∴CE=CF.
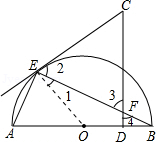
∵EC是切线,E为切点,
∴EO⊥EC,
∴∠1+∠2=90°,
∵AB是半圆O的直径,CD垂直AB于D,
∴∠FDB=90°,
∴∠FBD+∠4=90°,
∵∠1=∠FBD,∠3=∠4,
∴∠4=∠3=∠2,
∴CE=CF.

根据EC是切线,E为切点得出EO⊥EC,再利用∠FBD+∠4=90°,进而得出∠CEF=∠CFE,即可得出答案.

练习册系列答案
相关题目

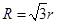 ;
;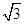 ,则⊙O的半径为【 】.
,则⊙O的半径为【 】.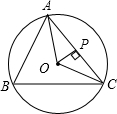
 、
、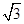 ,则
,则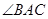 =
=  .
.
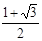 B.
B.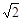 C.
C.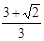 D.
D.